Вывод уравнений Лагранжа 2-го рода.

Рассмотрим движение системы из N мат. точек относительно инерциальной системы отсчета. Если некоторые связи не идеальные, то соответствующие им реакции следует добавить к действующим на систему активным силам.

Общее уравнение динамики для такой системы имеет вид

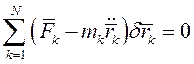(1)

Пусть система имеет n степеней свободы и её положение определяется 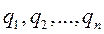обобщенными координатами 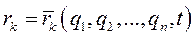. Возможное перемещение k-й точки

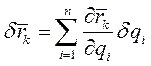(2)

Подставляя (2) в (1) и изменяя порядок суммирования получаем

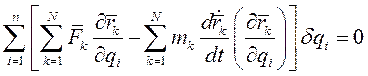(3)

В этом выражении 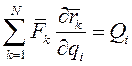- обобщенная сила, соответствующая i-й координате. Преобразуем выражение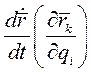

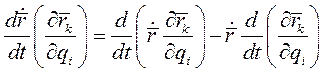(4)

Так как 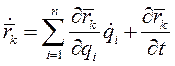, то

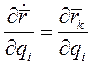(5)

Равенство (4) называется первым тождеством Лагранжа.

Заменив на основании этого тождества производную 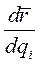на 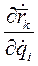в первом слагаемом выражения (5), получим

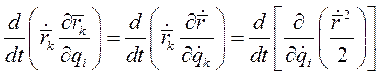
Следовательно

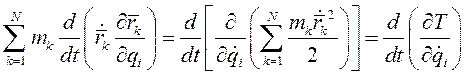(I)

Где Т – кинетическая энергия механической системы

Преобразуем теперь производную 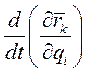. Так как 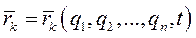, то 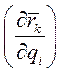- функция обобщенных координат и времени. Поэтому, с одной стороны,

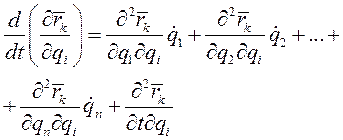(6)

С другой стороны

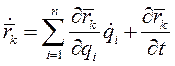
и

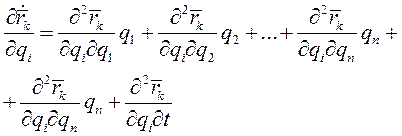(7)

Сопоставляя (5) и (6) заключаем, что

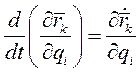(8)

Это второе тождество Лагранжа.

М учетом данного тождества получаем

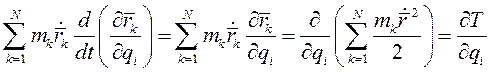(II)

Подставляя в общее уравнение (3) выражение для обобщенной силы 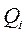б а также результаты преобразований (I) и (II), находим

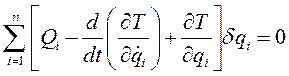(III)

Вариации обобщенных координат независимы между собой, поэтому условие (III) будет выполнено, если равны нулям множители при всех 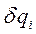, т.е. если

(*)

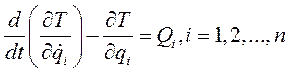Уравнения (*) называются уравнениями Лагранжа второго рода.