Эллипсоид инерции. Главные оси инерции симметричных твёрдых тел.

Эллипсоид инерции – поверхность второго порядка, построенная в любой точке тела – характеризует спектр моментов инерции тела относительно осей, проходящих через эту точку.

Для построения этой поверхности на каждой из оси Ol, проходящей через точку О, откладывают от этой точки отрезок

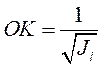
Главные оси (симметрии) эллипсоида инерции, построенного в точке твёрдого тела, называют главными осями инерции для данной точки тела.

Если оси координат направить по взаимно перпендикулярным главным осям эллипсоида инерции (OX, OY, OZ), то его уравнение будет иметь вид

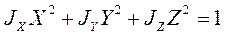(1)

Эллипсоид инерции, построенный для центра масс тела, называется центральным эллипсоидом инерции, а его главные оси – главными центральными осями инерции тела. В формуле это 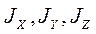. Моменты инерции относительно главных центральных осей инерции называют главными центральными моментами инерции тела и обозначают

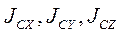. Сравнив (1) с уравнением эллипсоида в канонической форме

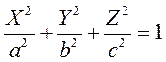
получим

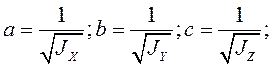
Эллипсоид называется трёхосным, если все главные моменты инерции для точки тела различны, и эллипсоидом вращения, если два главных момента инерции для точки тела равны.

36. Кинетический момент твёрдого тела, вращающегося вокруг неподвижной точки.

37. Кинетическая энергия твёрдого тела при движении вокруг неподвижной точки.

38. Вывод кинематических и динамических уравнений Эйлера.

39. Приближённая теория гироскопа. Основные понятия и допущения.

40. Особенности движения оси гироскопа. Теорема Резаля. Правило прецессии.

41. Гироскопический момент. Правило Жуковского.