Связи и их классификация.

Механическая система, точки которой могут занимать любое положения в пространстве и иметь любые скорости, называется свободной.

Если на координаты и скорости точек системы наложены ограничения, то система называется несвободной, а ограничениями называются связями.

Аналитически связь описывается уравнением вида

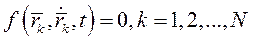
Ограничивая движения механической системы, связи действуют на её точки посредством сил, которые называются реакциями связей.

При изучении равновесия и движения механических систем методами аналитической механики применяется принцип освобождения (аксиома о связях)

Связи называются голономными, если они описываются уравнениями вида

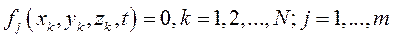(I)

Такие связи накладывают ограничения на координаты точек, а значит, на положение системы в пространстве.

Неголономными называются связи, которые описываются уравнениями вида

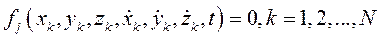(II)

Уравнения (I), в отличие от уравнений голономных связей, не могут быть проинтегрированы независимо от дифференциальных уравнений движения системы. Неголономные связи накладывают ограничения на скорости точек, поэтому их называют кинематическими.

Связи подразделяют на стационарныеи нестационарные в зависимости от того, входит в явном виде время в уравнение связи или нет.

Связь, уравнение которой имеет вид , является голономной и стационарной. Для голономной нестационарной связи уравнение будет таким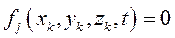

Связь называется удерживающей (двухсторонней), если она описывается уравнением (равенством).

Неудерживающая (односторонняя) связь описывается неравенством.