Теорема об изменении кинетической энергии для точки и системы материальных точек.
В дифф. форме:
Дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.
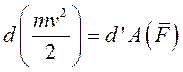
|
В интегральной форме:
Изменение кинетической энергии точки на любом перемещении равно работе силы, действующей на точку, на том же перемещении.
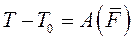
|
Движение точки массой m под действием силы 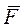 определяется уравнением
определяется уравнением
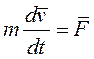
или
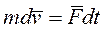
Умножив обе части уравнения скалярно на 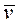 , после преобразований
, после преобразований
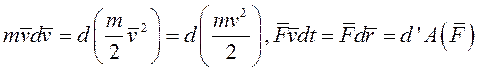
получим
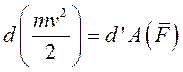
Разделив обе части уравнения на dt, получим ещё одну запись теоремы об изменении кинетической энергии точки
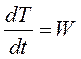
Интегрируя обе части по криволинейной траектории 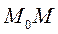 имеем
имеем
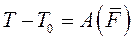
Теорема об изменении кинетической энергии для механической системы.
Дифф. форма:
Дифференциал кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.
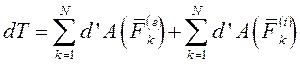
Первая производная по времени от кинетической энергии системы равна сумме мощностей всех внешних и внутренних сил, действующих на точки системы
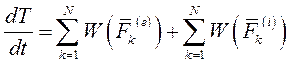
В интегральной форме
Изменение кинетической энергии системы при её перемещении из одного положения в другое равно суме работ всех внешних и внутренних сил, действующих на систему, на соответствующих перемещениях точек приложения этих сил.
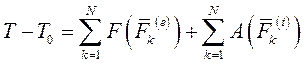
Для механической системы, на которую действуют как внешние, так и внутренние силы, уравнение 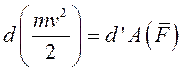 можно представить в виде
можно представить в виде
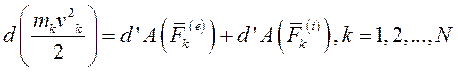 (I)
(I)
Суммируя левые и правые части этих уравнений по всем точкам системы и вынося знак дифференциала за знак суммы, получаем
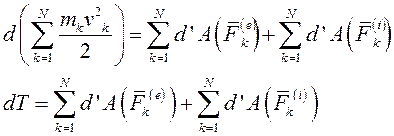
Разделим обе части уравнения на dt
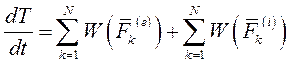
Проинтегрируем каждое уравнение (I) по соответствующей ему криволинейной траектории. Просуммировав полученные выражения по все точкам системы, получим
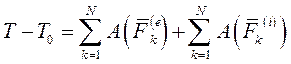
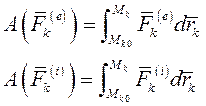
Дата добавления: 2021-07-22; просмотров: 501;











