Определение углового положения систем координат с помощью направляющих косинусов

Направляющими косинусами 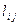осей системы 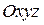относительно осей системы координат 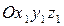называются косинусы углов между соответствующими осями систем.

Например (рис.22):

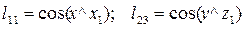
Матрица направляющих косинусов

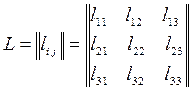
однозначно определяет условное положение системы координат 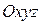относительно системы координат 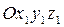. Координаты точки с известными их значениями в прямоугольной системе 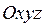при переходе к системе 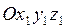преобразуются с помощью матрицы L

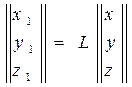
В координатной форме эти преобразования записываются в виде:

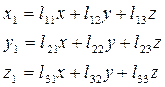
Орты 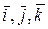системы 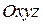и орты 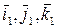связаны соотношениями:

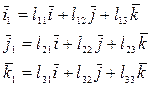
или

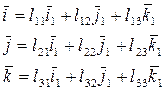
Соотношения между углами двух систем координат

Система координатных осей	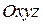Конусы углов между осями
x1	y1	z1
x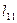
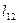
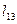
y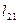
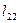
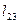
z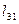

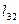
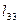
Свойства определителя преобразования

В силу ортогональности преобразования на направляющие косинусы накладывается 6 условий:

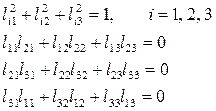
Определитель преобразования 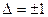(плюс, если левая система перешла в левую или правая в правую; минус, если левая перешла в правую и наоборот)