Некоторые сведения из алгебры матриц
Прямоугольная таблица, составленная из элементов (в частном случае чисел) и имеющая m строк и n столбцов, называется матрицей размера m x n. Элементы этой матрицы обозначаются через 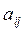 , где i – номер строки, а j – номер столбца, на пересечении которых находится этот элемент:
, где i – номер строки, а j – номер столбца, на пересечении которых находится этот элемент:

Если в матрице число строк не равно числу столбцов, то есть m¹n, то матрица называется прямоугольной. Матрица, имеющая только одну строку, то есть m=1, называется матрицей-строкой (или вектором-строкой):
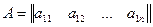
Матрица, имеющая только один столбец, то есть n=1, называется матрицей-столбцом (или вектором-столбцом):
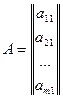
Матрицу-строку или матрицу-столбец называют вектором и обозначают
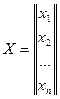 или
или 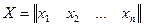 .
.
Числа х1, х2, …, хn называются координатами (или элементами) вектора Х. так как число координат вектора есть, по определению, его размерность, то вектор Х является n-мерным. Трёхмерный вектор R обозначается:
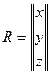 .
.
Если в матрице число строк равно числу столбцов, то есть m=n, то матрица называется квадратной.
Главной диагональю квадратной матрицы называется диагональ, проходящая через верхний левый и нижний правый углы, то есть совокупность элементов вида aii, где i=1,2,…,n.
Квадратная матрица, у которой все элементы, расположенные вне главной диагонали, равны нулю, называется диагональной. Эта матрица имеет следующий вид:
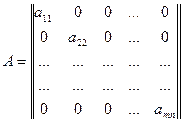
Диагональная матрица, у которой все элементы, стоящие на главной диагонали, равны единице, называется единичной. Единичная матрица обозначается:
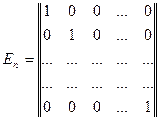
Индекс n указывает на порядок единичной матрицы.
Квадратная матрица, в которой все элементы расположены симметрично относительно главной диагонали, называется симметричной. Для симметричной матрицы aij=aji (i¹1), например:

Матрица, все элементы которой равны нулю, называется нулевой и обозначается через О. если нужно указать число строк и столбцов, то записывают:
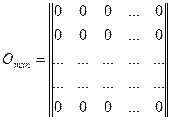
Две матрицы 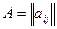 и
и 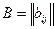 называются равными, если: 1) они одного и того же размера; 2) соответствующие элементы этих матриц равны между собой. Таким образом, если:
называются равными, если: 1) они одного и того же размера; 2) соответствующие элементы этих матриц равны между собой. Таким образом, если:
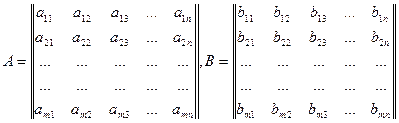
и aij=bij (i=1,2,…,m; j=1,2,…,n.), то А=В.
Суммой двух матриц одного и того же размера 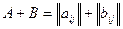 называется матрица
называется матрица 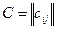 того же размера, элементы которой Сij равны суммам соответствующих элементов aij=bij матриц А и В, то есть сij=aij+bij.
того же размера, элементы которой Сij равны суммам соответствующих элементов aij=bij матриц А и В, то есть сij=aij+bij.
Разность матриц определяется аналогично сумме, только у элементов вычитаемой матрицы знак меняется на противоположный: D=A-B; dij=aij-bij (i=1,2,…,m; j=1,2,…,n.).
Произведением матрицы 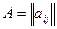 на число a называется матрица, элементы которой получаются умножением всех элементов матрицы на число a:
на число a называется матрица, элементы которой получаются умножением всех элементов матрицы на число a:
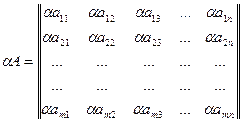
Матрица –А=(-1)А называется противоположной матрице А.
Сложение матриц подчиняется следующим законам:
А+(В+С)=(А+В)+С; А+В=В+А; А+0=А; А+(-А)=0.
Произведение матрицы на число подчиняется следующим законам:
1×А=А; 0×А=0; a(bА)=(ab)×А.
Произведением А×В двух матриц:
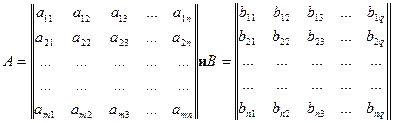 ,
,
имеющих соответственно размеры m x n и n x q, называется матрица
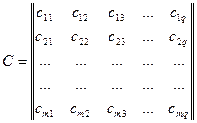
размера m x q. Матрица С= А×В определена только тогда, когда число столбцов матрицы А равно числу строк матрицы В. Чтобы получить элементы сij, стоящий в i-й строке и j-м столбце произведения двух матриц, нужно элементы i-й строки первой матрицы умножить на соответствующие элементы j-го столбца второй и полученные произведения сложить:
сij=ai1b1j+ ai2b2j+…+ ainbnj (i=1,2,…,m; j=1,2,…,n.).
Например, с23=a21b13+ a22b23+…+ a2nbn3, с41=a41b11+ a42b21+…+ a4nbn1, и т.п.
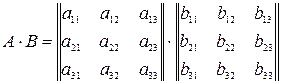 =
=
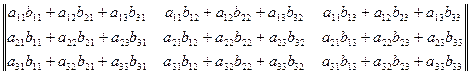
Произведение матриц подчиняется следующим законам:
А(ВС)=(АВ)С; a(АВ)=(aА)В; (А+В)С=АС+ВС; ЕА=А; АВ¹ВА; АЕ=ЕА=А.
Действия сложения и умножения на число над матрицами-столбцами и матрицами-строками (т.е. векторами) производятся аналогично соответствующим действиям над квадратными матрицами. Суммой двух векторов 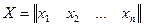 и
и  является вектор
является вектор 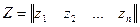 с координатами z1=x1+y1; z2=x2+y2; … ; zn=xn+yn; произведением вектора
с координатами z1=x1+y1; z2=x2+y2; … ; zn=xn+yn; произведением вектора 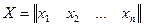 на число a - вектор
на число a - вектор 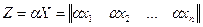 .
.
Транспонированной матрицей размера n x m называется матрица (размера n x m), полученная из матрицы А размера m x n путём замены строк соответствующими столбцами.
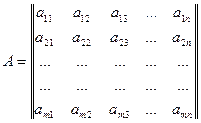
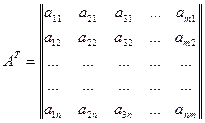
Свойства операции транспонирования:
(АТ)Т=А; (А+В)Т=АТ+ВТ; (А×В)Т=ВТ×АТ.
Определителем третьего порядка называется число
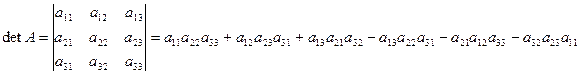
Свойства определителя:
1) определитель не меняется при транспонировании;
2) если одна из строк или один из столбцов определителя состоит из нулей, то определитель равен нулю;
3) при перестановке двух строк или двух столбцов определитель меняет только знак;
4) определитель, содержащий две одинаковые строки или два одинаковых столбца, равен нулю;
5) если все элементы некоторой строки или столбца определителя умножить на число R¹0, то сам определитель умножится на это число;
6) определитель, содержащий две пропорциональные строки, равен нулю;
7) если все элементы i-й строки определителя n-го порядка представить в виде суммы двух слагаемых: aij=bij+cij (i=1,2,…,n) то данный определитель равен сумме двух определителей, у которых все строки, кроме i-й, такие же, как и в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bij, а в другом – из элементов cij;
8) если одна из строк определителя представляет собой сумму каких-либо других строк или сумму произведений каких-либо других строк определителя на число k, то определитель равен нулю;
9) определитель не изменится, если к элементам одной из его строк (столбцов) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Квадратная матрица называется обратной по отношению к данной квадратной матрице, если её умножение как справа, так и слева на данную матрицу даёт единичную матрицу, то есть:
А×А-1=А-1×А=Е
Квадратная матрица называется неособенной (или невырожденной), если её определитель не равен нулю. Если же определитель матрицы равен нулю, то матрица называется особенной (или вырожденной).
Для того чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы определитель матрицы А был отличен от нуля, то есть чтобы матрица А была неособенной.
Матрица, составленная из алгебраических дополнений и затем протранспонированная называется союзной (или присоединённой) по отношению к исходной матрице А и обозначается 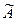 :
:

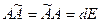
где d – определитель матрицы.
В общем виде для квадратной матрицы n-го порядка обратная матрица вычисляется по формулам:
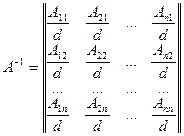
то есть элементы исходной и обратной матриц связаны соотношением 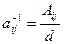 .
.
Для матрицы третьего порядка:
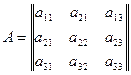 ,
, 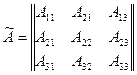
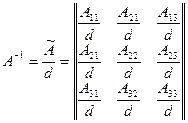
Дата добавления: 2017-05-02; просмотров: 1756;











