Элементарные преобразования координат

Случаи или преобразования координат называются элементарными, если:

1) для полного совмещения осей координат необходим только поворот вокруг одной из осей; в этом случае начала систем координат совпадают, а ось поворота является общей для обеих систем (рис. 23)

Для случая элементарного поворота связь между координатами точки в системах координат 1 и 2 определяется формулой 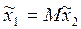, где 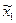- координаты точки в системе 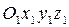; 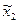- координаты той же точки в системе координат 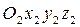; 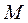- матрица поворота. При этом положительным направлением отсчета угла следует считать отсчет по часовой стрелке при условном перемещении оси с индексом i+1 к одноименной оси с индексом I (от оси x₂ к оси x₁).

2) для полного совпадения осей необходимо выполнить перенос начала системы 2 вдоль одной из осей координат; в этом случае оси системы 1 и 2 параллельны и одна из пар одноименных осей систем направлена в одну сторону по одной общей прямой (рис. 24)

Для случая поворота относительно оси x матрица имеет вид:

,

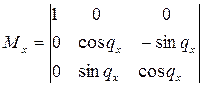где 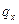- угол поворота относительно оси x.

Для поворота относительно оси y матрица имеет вид:

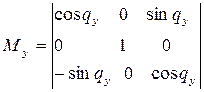
где 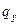- угол поворота относительно оси y.

Относительно оси z:

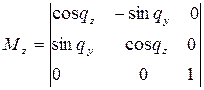
Обычно в механике положительным считается поворот, происходящий против часовой стрелки, если смотреть с острия оси, вокруг которой он происходит. При преобразовании координат путем условного поворота осей до их совмещения положительный угол отсчитывается по часовой стрелке.

Преобразование координат для случая элементарного переноса производится по формуле:

,

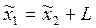где L – вектор, имеющий общий вид 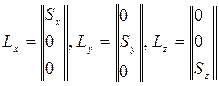соответственно смещению систем осей 1 и 2 относительно осей x, y, z.