А) Расчет рамы в системе пространственного блока при
Жесткой кровле
Под жесткой кровлей подразумевается распространенная в настоящее время кровля, которая состоит из крупноразмерных железобетонных плит, уложенных непосредственно на верхние пояса стропильных ферм и приваренных к ним. При выводе рабочих формул жесткость такого диска кровли принималась бесконечно большой. Жесткость продольных связей и тем более тормозных балок по сравнению с жесткостью кровли незначительна, и ею пренебрегалось, что идет в запас жесткости.
Определим деформации каркаса здания от местных (крановых) нагрузок в предположении, что все рамы в пределах температурного отсека или отсека условной длины связаны бесконечно жестким диском кровли в пространственный блок.
Заменим воздействие крановых сил на поперечные рамы пространственного блока эквивалентными силами, приложенными в верхних узлах. Для наиболее нагруженной рамы примем 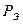 и для соседних
и для соседних 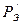 ,
, 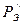 и т. д.
и т. д.
Рассмотрим сначала работу наиболее нагруженной рамы под воздействием силы 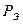 . Обозначив величину полного горизонтального смещения верхних узлов плоской рамы
. Обозначив величину полного горизонтального смещения верхних узлов плоской рамы 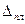 и
и 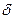 — смещение от Р=1, получим:
— смещение от Р=1, получим:
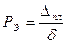 . (2.18)
. (2.18)
При воздействии крановых нагрузок или эквивалентной имсилы 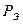 по оси блока рам смещение каждой из них (при одинаковой жесткости и шаге стоек) будет равно (рис. 2.12, а):
по оси блока рам смещение каждой из них (при одинаковой жесткости и шаге стоек) будет равно (рис. 2.12, а):
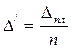 , (2.19)
, (2.19)
где 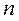 — число рам в блоке.
— число рам в блоке.
При внецентренном приложении силы 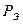 к блоку наряду с поступательным перемещением диск будет поворачиваться под воздействием вращающего момента:
к блоку наряду с поступательным перемещением диск будет поворачиваться под воздействием вращающего момента:
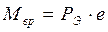 , (2.20)
, (2.20)
где е — эксцентриситет приложения силы по отношению к центру вращения (рис. 2.12, 6). Центр вращения при одинаковой жесткости и шаге стоек рам будет совпадать с геометрическим центром блока.
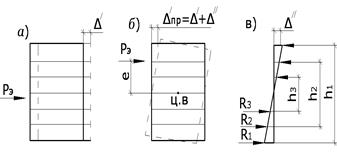
| Рис. 2.12. Перемещения жесткого диска кровли а — при приложении на грузки в центре тяжести диска; б — при внецентренном приложении на грузки; в — схема загружения диска кровли силами упругого отпора стоек рам |
Внешний момент уравновешивается суммой моментов упругих отпоров (рис. 2.12, б), поэтому
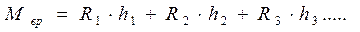
Из этого уравнения можно найти упругий отпор для любой рамы
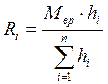 . (2.21)
. (2.21)
Зная упругий отпор и смещение рамы от силы, равной единице, получим выражение для смещения любой рамы блока от поворота:
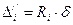 . (2.22)
. (2.22)
Подставив в эту формулу полученные ранее значения для 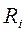 из формулы (2.21) и
из формулы (2.21) и 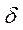 из формулы (2.18), получим
из формулы (2.18), получим
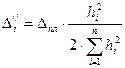 .
.
Полное смещение рамы по ряду 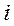 в системе пространственного блока при эксцентричном приложении эквивалентной силы
в системе пространственного блока при эксцентричном приложении эквивалентной силы 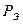 будет равно сумме:
будет равно сумме:

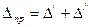
Подставляя в эту формулу полученные выше значения для 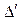 и
и 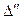 , получим
, получим
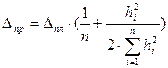 . (2.23)
. (2.23)
Формула (2.23) позволяет определить смещение верхних узлов рамы ряда 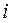 , возникающее в результате действия на пространственный блок силы
, возникающее в результате действия на пространственный блок силы 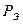 . Но на блок рам, соединенных жестким диском кровли, кроме силы
. Но на блок рам, соединенных жестким диском кровли, кроме силы 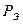 действуют еще и силы
действуют еще и силы 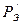 ,
, 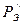 ... Дополнительные смещения рамы ряда
... Дополнительные смещения рамы ряда 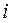 от
от 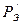 и
и 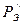 можно получить аналогичным путем. Однако проще учесть их введением в формулу (2.23) коэффициента
можно получить аналогичным путем. Однако проще учесть их введением в формулу (2.23) коэффициента 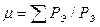 или, воспользовавшись пропорциональностью между
или, воспользовавшись пропорциональностью между 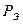 и
и 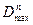 принять
принять 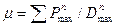 , где
, где 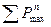 -сумма нормативных давлений колес двух кранов на один крановый рельс.
-сумма нормативных давлений колес двух кранов на один крановый рельс.
При выводе формулы (2.23) принималось, что диск кровли абсолютно жесткий. В действительности по ряду причин возможны сдвиги между отдельными плитами, что на первых порах, впредь до проведения соответствующих экспериментальных исследований, можно приближенно учесть введением коэффициента условий работы 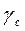 . Этим же коэффициентом будем учитывать увеличение жесткости кровли для многопролетных или без фонарных зданий.
. Этим же коэффициентом будем учитывать увеличение жесткости кровли для многопролетных или без фонарных зданий.
Рекомендуются следующие значения коэффициента условий работы: 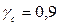 для однопролетных зданий с продольным фонарем и
для однопролетных зданий с продольным фонарем и 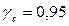 для двух- и трех пролетных зданий с фонарями или однопролетного — без фонаря.
для двух- и трех пролетных зданий с фонарями или однопролетного — без фонаря.
В многопролетных зданиях с жесткой кровлей (при четырех и более пролетах) смещения верхних узлов рамы будут малы, и ими можно пренебречь и рассчитывать плоскую раму с не смещающимися узлами.
Практически в этом случае на горизонтальные нагрузки рассчитывают отдельные стойки.
Из формулы (2.23) видно, что наибольшее значение 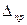 будет иметь наиболее удаленная от центра блока первая рама, расположенная в плоскости торца или температурного шва. Но так как первая рама не может быть загружена силой
будет иметь наиболее удаленная от центра блока первая рама, расположенная в плоскости торца или температурного шва. Но так как первая рама не может быть загружена силой 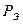 , соответствующей максимальному давлению
, соответствующей максимальному давлению 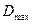 , то за расчетную следует принять вторую от торца или температурного шва раму.
, то за расчетную следует принять вторую от торца или температурного шва раму.
При шаге основных рам 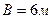 и кранах грузоподъемностью 1000 кН и более расчетной может быть не вторая, а третья рама. Однако в целях унификации метода расчета и упрощения формулы (2.24) за расчетную во всех случаях рекомендуется принимать вторую раму, что для указанного случая идет в запас прочности.
и кранах грузоподъемностью 1000 кН и более расчетной может быть не вторая, а третья рама. Однако в целях унификации метода расчета и упрощения формулы (2.24) за расчетную во всех случаях рекомендуется принимать вторую раму, что для указанного случая идет в запас прочности.
Подставив в формулу (2.23) коэффициенты μ, и m и обозначив
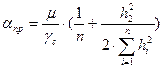 , (2.24)
, (2.24)
получим окончательную формулу
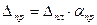 . (2.25)
. (2.25)
Коэффициент 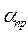 - будем называть коэффициентом пространственной жесткости каркаса. Определим коэффициент пространственной жесткости для примера 3.
- будем называть коэффициентом пространственной жесткости каркаса. Определим коэффициент пространственной жесткости для примера 3.
Число рам:
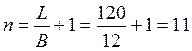 ,
,
где 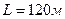 - длина здания;
- длина здания;
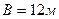 - шаг рам.
- шаг рам.
Коэффициент:
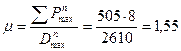 ;
;
Здесь: 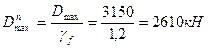 ;
;
коэффициент 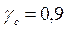 , тогда
, тогда
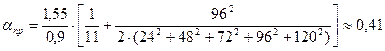 .
.
Дата добавления: 2017-09-01; просмотров: 2232;











