Связь между прямоугольными, цилиндрическими и сферическими

Координатами

Система координат	Система координат
Прямоугольная (x,y,z)	Цилиндрическая (r,j,z)	Сферическая (R,j,q)
Прямоугольная (x,y,z)	x=x y=y z=z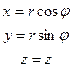
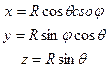
Цилиндрическая (r,j,z)		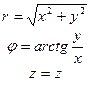r=r j=j z=z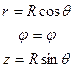
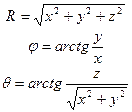
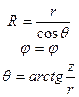
Сферическая (R,j,q)			R=R j=j q=q

Направление в пространстве характеризуется единичным вектором 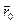или его координатами – косинусами углов (рис. 20), образованных заданными направлениями с положительными направлениями осей координат (направляющие косинусы); при этом

l=cosa; m=cosb; n=cosg; l²+m²+n²=1

Угол j между двумя заданными направлениями с направляющими косинусами l₁; m₁; n₁ и l₂; m₂; n₂ определяется из выражения cosj= l₁l₂+ m₁m₂+ n₁n₂

Если два направления перпендикулярны, то l₁l₂+ m₁m₂+ n₁n₂=0.

Переход от одной прямоугольной системы координат к другой прямоугольной системе координат можно осуществить при помощи параллельного переноса (до совмещения начала координат) и поворота системы относительно начала (до совмещения осей). Поворот прямоугольной системы координат можно описать с помощью направляющих косинусов, углов Эйлера, вектора конечного поворота, параметров Родрига-Гемильтона, параметров Кэли-Клейна и др.