Кинематический анализ манипуляторов методом проекций
Произведём анализ манипулятора типа «механическая рука», используемого для захвата и извлечения изделий из рабочей зоны и выдачи их на следующую позицию обработки.
Манипулятор робота представляет собой плоский механизм с захватом в точке Д. В заданной системе координат точка Д движется согласно уравнениям:
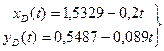 (38)
(38)
в течение 1с. На рис. 16 изображён в начальном положении механизм манипулятора и показаны положительные направления отсчёта углов j, y, q и расстояния S. Размеры звеньев: а=1,30 м, b=1,10 м, с=0,55 м.
В начальный момент времени (t=0).
j =j0=62°; y=y0=33°
Определить значения углов j, y, q и расстояния S для указанного промежутка времени. Вычислить также угловые скорости 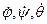 , угловые ускорения
, угловые ускорения 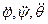 , относительную скорость
, относительную скорость 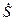 и относительное ускорение
и относительное ускорение 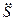 точки В. Вычисления произвести для моментов времени 0; 0,2; 0,4; 0,6; 0,8; 1с.
точки В. Вычисления произвести для моментов времени 0; 0,2; 0,4; 0,6; 0,8; 1с.
Для любого положения механизма справедливы векторные соотношения:
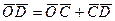 (39)
(39)
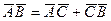 (40)
(40)
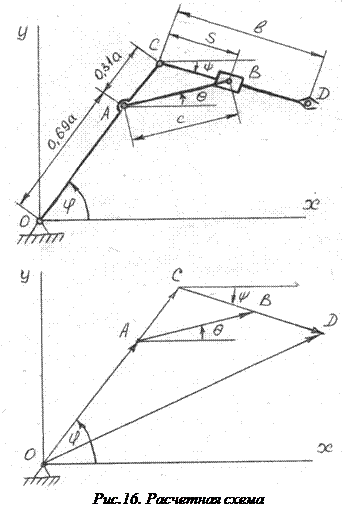 Где
Где 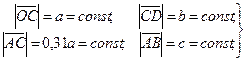 (41)
(41)
Равенства (38)…(41) являются уравнениями связей, наложенных на систему. Спроецируем (39) и (40) на оси координат:
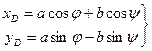 (42)
(42)
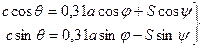 (43)
(43)
Продифференцировав (42) и (43) дважды по времени, учитывая (41), получим алгебраические уравнения относительно неизвестных угловых скоростей 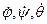 и скорости
и скорости 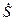 после первого дифференцирования и алгебраические уравнения относительно угловых ускорений
после первого дифференцирования и алгебраические уравнения относительно угловых ускорений 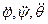 и относительного ускорения
и относительного ускорения 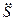 , связывающие их между собой после второго дифференцирования.
, связывающие их между собой после второго дифференцирования.
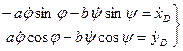 (44)
(44)
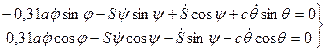 (45)
(45)
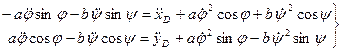 (46)
(46)
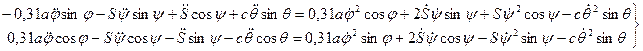
Величины 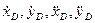 входящие в выражения (44) и (46) определяются дифференцированием уравнений движения схвата (38):
входящие в выражения (44) и (46) определяются дифференцированием уравнений движения схвата (38):
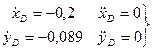 (47)
(47)
Для начального момента времени t=t0=0 системы уравнений (44) и (45) имеют следующий вид:
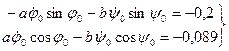 (48)
(48)
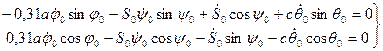 (49)
(49)
Для определения S0 и q0 воспользуемся системой (43) для начального положения (t=0)
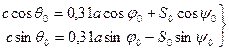
Разделив данную систему относительно S0 и tgq0, получим
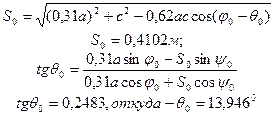
Подставляя значения a, b, c, j0, y0, q0, S0 в (48), (49), получим систему уравнений
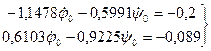
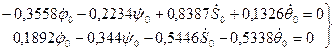
Решая эту систему уравнений, получим:
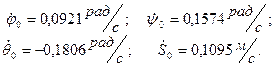 (50)
(50)
Используя найденные результаты, составим систему для начального положения уравнений (46):
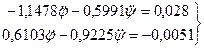
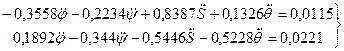
Решая эту систему уравнений, получим:
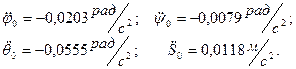 (51)
(51)
Следующий момент времени, при котором необходимо определить искомые величины, является t=t1=Dt=0,2 с. Считая Dt малой величиной можно записать:
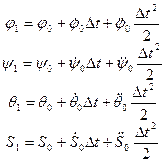 (52)
(52)
Выражение (52) непосредственно вытекает из разложения функций j(t), y(t), q(t), S(t) в ряд Макларена в окрестности t=0. В результате вычислений:
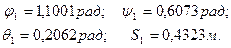
В общем случае переход от ji, yi, qi, Si к ji+1, yi+1, qi+1, Si+1 будет осуществляться по формулам:
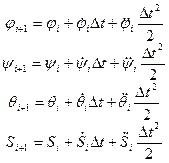 (53)
(53)
где i – порядковый номер рассчитываемого положения механизма. Уравнения (53) соответствуют закону изменения параметров j, y, q, S в интервале времени [ti, ti+1] с постоянным ускорением (равномерное движение).
По найденным согласно (52) j1, y1, q1, S1 вновь строим системы уравнений (44) и (45) относительно неизвестных 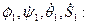
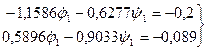
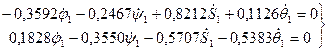
Решая эту систему уравнений, получим:
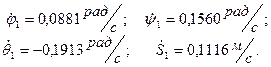
Используя полученные результаты, опять составляем системы уравнений (46) и (47) относительно неизвестных 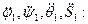
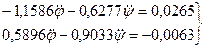
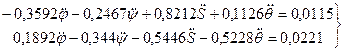
Решая эту систему уравнений, получим:
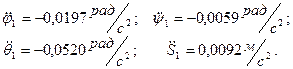
Очередным моментом времени, при котором необходимо определить величины, является t=t2=2Dt=0,4 с.
Воспользовавшись (53), при i=1 найдём j2, y2, q2, S2.
Описанная выше вычислительная процедура выполняется k раз, где
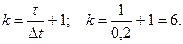
Здесь t - длительность процесса движения (t=1с).
После проведения всех вычислений составляется таблица значений 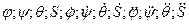 для всех различных моментов времени.
для всех различных моментов времени.
Дата добавления: 2017-05-02; просмотров: 1646;











