Дискретные случайные величины

Пусть имеются основания предположить, что изучаемая величина Х распределена по некоторому дискретному закону. Чтобы проверить, согласуется ли это предположение с данными наблюдений, вычисляют частоты наблюдаемых значений, т.е. находят теоретически частоту 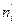каждого из наблюдаемых значений в предположении, что величина Х распределена по предполагаемому закону.

Выравнивающими (теоретическими) называют частоты 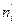, определяемые расчетным способом:

,

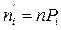где n – объем выборки;

P_i – вероятность наблюдаемого значения x_i, вычисленная при допущении, что Х имеет предполагаемое распределение.

Пример 7.5. По данным примера 7.3 определить теоретические частоты 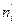в предположении, что случайная величина Х (генеральная совокупность) распределена по закону Пуассона. Построить полигон эмпирических и теоретических частот.

Решение

Пользуясь полученной в примере 7.3 формулой, найдем соответствующие вероятности при k= x_i, затем, перемножив их на n, получим соответствующие теоретические частоты. Результаты расчетов представим в виде таблицы:

Таблица 6