Показатели вариации

При решении практических задач оценка рассеяния (вариации) значений рассматриваемого признака может оказаться не менее важной, чем определение средней величины или структурных характеристик.

Под вариацией в статистике понимается – многообразие, колеблемость, изменяемость значений признака в рассматриваемой совокупности.

Показатели вариации можно разбить на две группы: абсолютные и относительные показатели.

К абсолютным показателям вариации относят: 1) размах вариации (вариационныйразмах); 2) среднеелинейноеотклонение; 3) дисперсия; 4) среднееквадратическоеотклонение (стандартное отклонение).

1. Размах вариации (вариационный размах) – разность между наибольшей и наименьшими вариантами ряда:

.

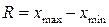2. Среднеелинейноеотклонение вариационного ряда – это средняя арифметическая абсолютных отклонений вариантов от их средней арифметической:

.

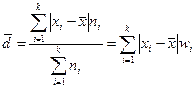3. Дисперсия – это средний квадрат отклонений вариантов от их средней арифметической:

.

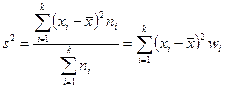Основными свойствами дисперсии являются:

3.1. Дисперсия постоянной величины равна нулю.

3.2. Если все варианты увеличить (уменьшить) в одно и то же число с раз, то дисперсия увеличится (уменьшится) в с² раз:

,

,

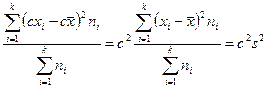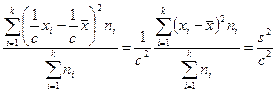где с ≠ 0 – const.

3.3. Если все варианты увеличить (уменьшить) на одно и то же число, то дисперсия не изменится:

.

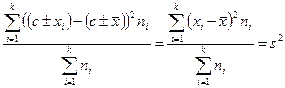где с – const.

3.4. Средний квадрат отклонений вариантов от их средней арифметической меньше, чем от любой другой постоянной величины:

,

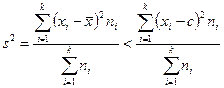или

,

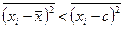причем

,

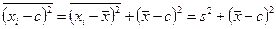где с – const.

3.5. Дисперсия равна разности между средней арифметической квадратов вариантов и квадратом средней арифметической:

.

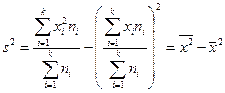3.6. Если ряд состоит из нескольких групп наблюдений, то общая дисперсия равна сумме межгрупповой дисперсии и средней из групповых дисперсий (правило сложения дисперсий):

,

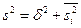где 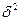- межгрупповая дисперсия, 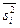- средняя из групповых дисперсий.

,

,

,

,

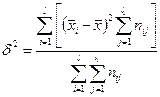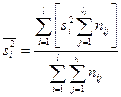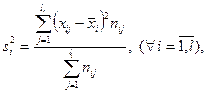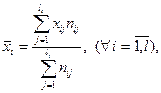где l – количество групп, на которые разбит ряд;

l_i – численность вариантов i-ой группы ( );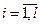

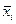- средняя арифметическая i-ой группы (групповая средняя) ( );

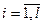n_ij – частота j-ого варианта, принадлежащего i-ой группе ( ; );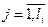

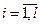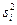- групповая дисперсия ( ).

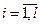4. Среднее квадратическое (стандартное) отклонение - арифметическое значение корня квадратного из дисперсии:

.

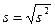Необходимо различать дисперсию и стандартное отклонение генеральной совокупности (генеральная дисперсия, генеральное среднее квадратическое отклонение) и выборки (выборочная дисперсия, выборочное среднее квадратическое отклонение). Последние рассчитываются оп опытным (выборочным) данным и являются точечными оценками соответствующих характеристик генеральной совокупности. В дальнейшем генеральную среднюю дисперсию будем обозначать 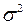, генеральное среднее квадратическое отклонение - 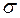, выборочную дисперсию – s², выборочное среднее квадратическое отклонение - s.

Дисперсия и среднее квадратическое отклонение имеют большое значение в статистике, в частности, при анализе статистических распределений. К примеру, если исследуемая совокупность подчинена нормальному закону (или близкому к нему), то существует следующая зависимость между величиной среднего квадратического отклонения (а также вариационным размахом) и числом наблюдений:

· в пределах 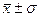располагается 68,3% единиц совокупности;

· в пределах 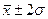располагается 95,45% единиц совокупности;

· в пределах 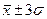располагается 99,7% единиц совокупности (практически вся совокупность).

Данное правило в статистике получило название «правило трех сигм».

Относительными показателями вариации являются: 1) коэффициент осцилляции; 2) линейныйкоэффициентвариации; 3) коэффициентвариации.

Относительные показатели вариации представляют собой отношение определенного абсолютного показателя вариации к среднему арифметическому, т.е. выражают вариацию признака в долях средней арифметической.

1. Коэффициент осцилляции:

.

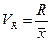2. Линейный коэффициент вариации:

.

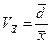3. Коэффициент вариации:

.

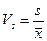Для удобства интерпретации относительные показатели вариации выражают в процентах.