Структурные характеристики статистических рядов

Основными структурными характеристиками статистических рядов являются мода и медиана.

Важнейшей характеристикой центра распределения, кроме средней арифметической, является мода.

Мода – значение признака, повторяющееся с наибольшей частотой в рассматриваемом статистическом ряду.

Для дискретного ряда мода находится непосредственно по вышеприведенному определению.

Для интервального ряда мода определяется по следующим формулам:

а) при равной ширине интервалов:

,

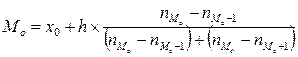где x₀ – нижняя (левая) граница модального интервала (в качестве модального принимают интервал, имеющий наибольшую частоту);

h – ширина интервалов;

n_Mo-1, n_Mo, n_Mo+1 – частоты интервалов, соответственно предшествующего модальному, модального и следующего за модальным.

б) при неравной ширине интервалов:

,

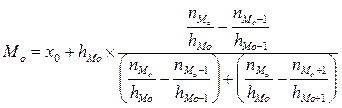где h_Mo-1, h_Mo, h_Mo+1 – ширина интервалов, соответственно предшествующего модальному, модального и следующего за модальным (в качестве модального принимают интервал, имеющий максимальную плотность частоты, т.е. );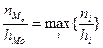

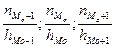- плотность частоты интервалов, соответственно предшествующего модальному, модального и следующего за модальным.

Задачи, связанные с отысканием моды, обычно решаются применительно к одновершинным (одномодальным) распределениям.

В статистическом анализе часто применяют структурные (порядковые) средние, например медиану. В отличие от средней арифметической, на которую оказывают влияние все значения исследуемого ряда распределения, структурные средние не зависят от крайних значений признака.

Медиана – значение признака, которое приходится на середину ранжированной совокупности (вариационного ряда).

Для дискретных не сгруппированных рядов номер медианного варианта определяется по следующей формуле:

.

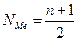Если количество вариантов четное, то номер медианной варианты будет дробным, а медиана будет расположена между двумя серединными вариантами. В данном случае медиана определяется как половина суммы двух серединных вариантов.

В случае нечетного количества вариантов, медиана соответствует варианте под номером N_Me.

Для дискретных сгруппированных рядов медиана определяется по накопленным частотам, т.е. медианой будет та варианта, накопленная частота которой первой превысит половину суммы частот рассматриваемого ряда.

В случае статистических рядов интервального типа медиана определяется по следующей формуле:

,

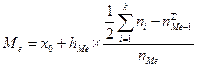где 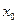- нижняя (левая) граница медианного интервала (в качестве медианного принимают интервал, накопленная частота которого первой превысит половину суммы частот рассматриваемого ряда);

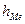- ширина медианного интервала;

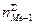- накопленная частота интервала, предшествующего медианному;

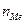- частота медианного интервала.

Пример. В результате выборочного наблюдения было установлено следующее распределение магазинов города по размеру среднемесячного товарооборота:

Таблица 2