Непрерывные случайные величины

В случае непрерывного распределения, вероятности отдельных возможных значений равны нулю. Поэтому весь интервал возможных значений делят на k непересекающихся интервалов и вычисляют вероятности P_i попадания случайной величины X в i-ый частичный интервал, а затем, как и для дискретного распределения, умножают число испытаний на эти вероятности, т.е.

,

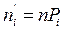где n – объем выборки;

P_i – вероятность попадания случайной величины Х в i-ый частичный интервал, вычисленная при допущении, что Х имеет предполагаемое распределение.

К примеру, если имеются основания предположить, что случайная величина Х (генеральная совокупность) подчинена нормальному закону распределения, то вероятность попадания случайной величины Х в i-ый частичный интервал P_i вычисляются по следующей формуле:

,

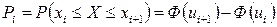где x_i, x_i+1 – границы i-го частичного интервала;

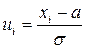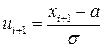; - нормированные величины;

a, σ – соответственно математическое ожидание и стандартное отклонение случайной величины X;

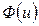- функция Лапласа (табличная величина, приложение), причем 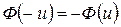- нечетная функция.

Пример 7.6.По данным примера 7.4определить теоретические частоты 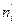в предположении, что случайная величина Х (генеральная совокупность) распределена по нормальному закону. Построить полигон эмпирических и теоретических частот.

Решение

Для расчета теоретических частот вычислим нормированные величины u_i; u_i+1:

1 интервал: -∞; ;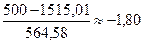

2 интервал: -1,80; ;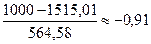

3 интервал: -0,91; ;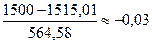

4 интервал: -0,03; ;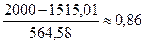

5 интервал: 0,86; ;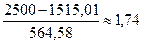

6 интервал: 1,74; ∞.

Таблица 7