Статистическое распределение выборки

Пусть из генеральной совокупности (объемом N), представляющей различные реализации изучаемого признака (случайной величины) Х, извлечена выборка объемом n, причем х₁ встречается n₁ раз, х₂ - n₂ раз, …, х_k - n_k раз, и .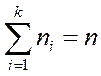

Значения x_i называют вариантами, а последовательность вариантов, записанных в возрастающем порядке, - вариационным рядом[1]. Числа n_i называют абсолютными частотами или просто частотами, а их отношения к объему выборки

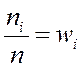- относительными частотами или частостями.

Наряду с частотами и относительными частотами выделяют также накопленные частоты 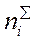- число наблюдений, в которых значения изучаемого признака не превосходят x_i. Накопленные частоты определяются следующим образом:

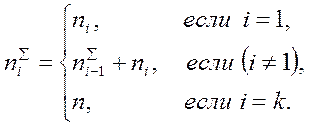
Статистическим распределением выборки (статистическим рядом) называют перечень вариантов и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот, в данном случае распределение будет интервального типа.

Статистическое распределение выборки может быть представлено в аналитической, табличной и графической формах.

Одной из аналитических форм представления статистического распределения выборки является эмпирическая функция распределения, определяющая для каждого значения x_i относительную частоту события 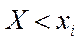, т.е.

.

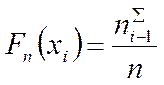Статистическое распределение выборки можно представить в табличной форме.

Таблица 1