Уравнение теплопроводности
Основной составляющей процесса передачи теплоты через ограждения является теплопроводность через материальные слои толщи ограждения. Процесс теплопроводности в материальных слоях конструкции подчиняется закону Фурье, уравнение которого в дифференциальной форме рассматривается в курсе тепломассообмена.
Вывод уравнения теплопроводности в конечных разностях проведем на примере одномерного температурного поля при передаче теплоты через однородную стенку (рис. 2.1). Толща стенки разбивается на элементарные слои размера Dх.
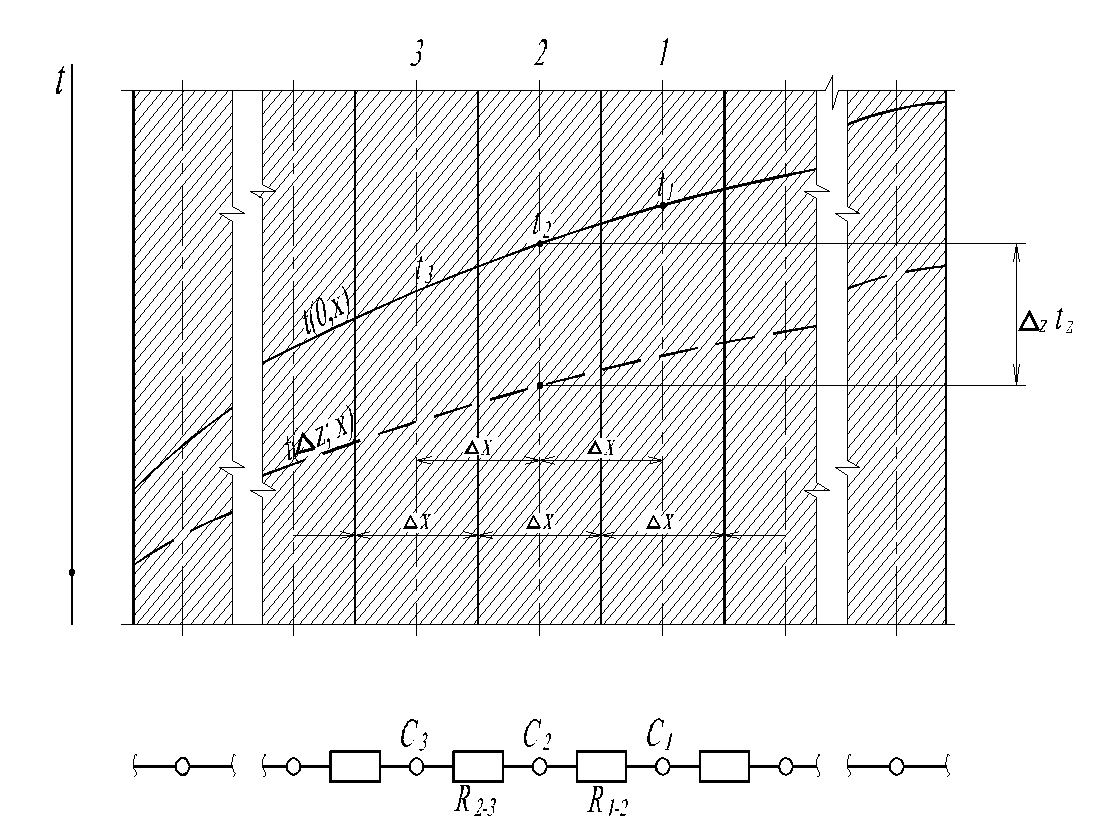
Рис. 2.1. К выводу уравнения теплопроводности в конечных разностях: а - непрерывное поле; б - тепловая цепочка
Процесс нестационарной передачи в толще определяется двумя законами: проводимости и аккумуляции теплоты.
Согласно закону проводимости тепловой поток q пропорционален градиенту температуры 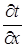 .
.
q = - l 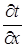 , (2.1)
, (2.1)
где l - коэффициент теплопроводности.
Знак "минус" показывает, что направление теплового потока противоположно направлению теплового градиента (направлению возрастания температуры). Для участка стены между осями элементарных слоев это уравнение можно написать в виде
q = 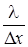 (t1 - t2), (2.2)
(t1 - t2), (2.2)
где t1 и t2 - температуры на осях соседних элементарных слоев 1 и 2.
Уравнение (2.2) справедливо только для линейного распределения температур в условиях стационарной передачи теплоты.
При нестационарных условиях, учитывая криволинейное распределение температуры в слоях, уравнение проводимости может быть записано в виде
q = 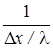 (t1 - t2), (2.3)
(t1 - t2), (2.3)
где 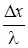 = R1-2 - сосредоточенное термическое сопротивление между сечениями 1 и 2.
= R1-2 - сосредоточенное термическое сопротивление между сечениями 1 и 2.
Уравнение (2.3) справедливо как для стационарных, так и для нестационарных (в отличии от 2.2) условий.
Закон аккумуляции теплоты устанавливает, что приращение количества теплоты dQ, аккумулированное слоем dх, пропорционально приращению во времени его температуры dt. Изменение количества аккумулированной теплоты DQ для элементарного слоя Dх при изменении во времени (z) его средней температуры на Dz t равно
DQ = сg Dх Dzt, (2.4)
где сg - объемная теплоемкость материала.
Составим уравнение теплового баланса элементарного слоя n при распределении температур в сечении, отмеченном на рисунке 2.1 индексом 1. Слой n обменивается теплотой с соседними элементарными слоями и, согласно закону проводимости, за время Dz он получит от слоя n + 1 количество теплоты
qn+1,n Dz = 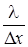 (tn+1 - tn) Dz, (2.5)
(tn+1 - tn) Dz, (2.5)
а отдаст слою n -1 количество теплоты
qn ,n-1 Dz = 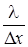 (tn - tn-1) Dz (2.6)
(tn - tn-1) Dz (2.6)
Разность DQn между количеством теплоты, определенными уравнениями (2.5) и (2.6), будет аккумулирована слоем n и повысит его среднюю температуру (формула 2.4) на Dz tn.
Уравнение теплового баланса слоя n можно записать
сg Dх Dz tn = 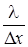 [(tn+1 - tn) - (tn - tn-1)]Dz, (2.7)
[(tn+1 - tn) - (tn - tn-1)]Dz, (2.7)
которое после преобразований может быть записано:
сg 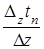 =
= 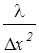 D2х tn, (2.8)
D2х tn, (2.8)
где
D2х tn = (tn+1 - tn) - (tn - tn-1) = Dtn+1,n - Dtn ,n-1 = tn+1 + tn-1 -2tn (2.9)
является второй конечной разностью температур, т.е. разностью разностей температур между элементарными слоями. Индекс х показывает, что имеется в виду изменение температуры в пространстве по координате х.
При переходе к пределу и замене конечных разностей бесконечно малыми приращениями из уравнения (2.8) получаем дифференциальное уравнение Фурье:
сg 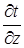 = l
= l 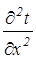 (2.10)
(2.10)
Дата добавления: 2021-07-22; просмотров: 518;











