Проверка адекватности математической модели

Проверка адекватности модели состоит в установлении возможности с помощью выбранной регрессионной модели объекта предсказывать с требуемой точностью значения выходной величины в некоторой области значений входной. Для этого прежде всего вычисляется оценка дисперсии адекватности

(28)

,

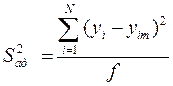где у_i – реальное значение выходной величины, полученное в результате i-го опыта,

у_im – значение выходной величины, предсказанное в i-м опыте по полученной модели (для получения у_im необходимо подставить в модель значения факторов, предусмотренные матрицей планирования в i-м опыте, вычислить значение у_im по значениям факторов и коэффициентов модели);

f – число степеней свободы, равное числу различных опытов, результаты которых используются при подсчете коэффициентов модели, минус число определяемых коэффициентов.

Гипотеза об адекватности модели проверяется с помощью F-критерия:

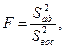(29)

где S²_вос – оценка дисперсии воспроизводимости со своим числом степеней свободы.

Модель считается адекватной, если рассчитанное значение F не превышает табличного. При несоблюдении этого условия проводится корректировка модели, вновь определяются коэффициенты и проверяется ее адекватность.

Решение о проведении дальнейших исследований принимается в зависимости от возможной ситуации.

1. Если коэффициенты регрессии значимы и линейная модель адекватна, то модель объекта можно считать построенной. При условии близости отклика к оптимальному значению f_min исследования можно закончить.

2. Если все коэффициенты регрессии незначимы (кроме b₀ ), а линейная модель адекватна, то необходимо расширить интервал варьирования или увеличить точность эксперимента (снизить S²_вос ) за счет большего числа параллельных опытов. Увеличение интервалов варьирования приводит к увеличению абсолютных величин коэффициентов регрессии.

3. Если линейная модель неадекватна, то это означает, что поверхность отклика не удается аппроксимировать плоскостью. В этом случае необходимо уменьшить интервалы варьирования, перенести нулевую точку варьирования или использовать более сложную модель - добавить взаимодействия факторов, т.е. перейти к нелинейным моделям. При сужении области экспериментирования необходимо помнить об ограничениях, накладываемых на минимальную величину Δx_j.

4. Если коэффициенты регрессии значимы, а план эксперимента является насыщенным, то адекватность проверить невозможно, т.к. в этом случае число степеней свободы, с которым определяется S²_ад , n-l=0 . Проверка возможна, если число коэффициентов модели меньше числа точек факторного пространства, в которых измерялся отклик. В этом случае можно провести дополнительные измерения в некоторой точке, например в x_o, тем самым увеличив n.