Решение задачи оптимизации

Задача оптимизации – это отыскание таких значений факторов х_1опт, х_2опт…х_{к опт}, при которых функция отклика (целевая функция) достигает экстремального значения:

у (х_1опт, х_2опт,…,х_{к опт}) = max(min) , (30)

при выполнении условий ограничения, число которых r может быть произвольным. Нахождение экстремума функции отклика производится при условии, что функция отклика априори неизвестна.

Решение поставленной задачи целесообразно вести путем поиска экстремума целевой функции. Для однофакторных экспериментов решение задачи сводится к нахождению производной.

Изучение поверхности отклика для многофакторного эксперимента производится последовательной постановкой нескольких серий опытов, каждая из которых производится с целью изучения ограниченных участков поверхности отклика и выбора направления движения, приближающего условия к оптимальным. Серии опытов продолжаются до тех пор, пока исследование не выведет на «почти стационарную область» вблизи точки оптимума. После этого ставится большая серия опытов с целью более точного описания поверхности отклика и нахождения точки оптимума.

Чтобы достичь экстремума за наименьшее число шагов, нужно двигаться по направлению наискорейшего возрастания целевой функции. Такого рода движение описывается с помощью вектора, называемого градиентом скалярного поля.

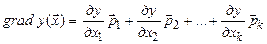, (31)

где 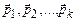– орты (единичные векторы) соответствующих координатных осей.

Сопоставляя (31) с линейной полиномиальной моделью, нетрудно сделать вывод, что координаты градиента 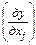совпадают с коэффициентами уравнения регрессии b₁, b₂ ,…,b_к и для максимальной скорости роста целевой функции необходимо двигаться в направлении градиента. Данное направление ортогонально линии равного уровня у(х)=const, проходящей через исходную точку х₀. Обычно считают, что линейная модель является хорошим приближением функции y(x) в некоторой окрестности x₀, ограниченной сферой радиуса

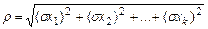, (32)

где sx_j –приращение факторов при удалении от исходной точки на фиксированное расстояние, равное r, j=1,2…k.

Для того чтобы определить, в каком направлении от точки x₀ в пределах r двигаться, чтобы получить максимальное приращение у(х), необходимо решить задачу на условный экстремум, т.е. найти такие sх_j, которые максимизируют

при r=const. (33)

Задача решается с помощью стандартного метода множителей Лагранжа. В результате решения получается

(34)

Выражение (34) представляет собой алгоритм поиска, так как задает линию наискорейшего подъема. Эта линия совпадает с направлением вектора градиента.

Таким образом, направление градиента функции отклика определяется значениями коэффициентов регрессии.

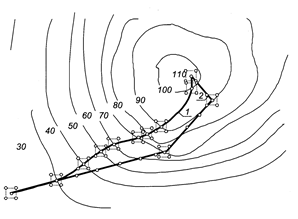
Поясним сущность метода градиента на примере двухфакторной функции отклика у (х₁, х₂). На рис. 5 в факторном пространстве изображены кривые равных значений функции отклика (кривые уровня). Если мы выберем какую-либо точку факторного пространства в качестве исходной (х₁₀, х₂₀), то наикратчайший путь к вершине функции отклика (область 110) на этой точке – это путь по кривой 1, касательная к которой в каждой точке совпадает с нормалью к кривой уровня, т.е. это путь в направлении градиента функции отклика. Реализация алгоритма движения по градиенту начинается с построения симметричного двухуровнего плана эксперимента относительно исходной точки х₁₀, х₂₀ факторного пространства. Интервалы варьирования при этом должны быть достаточно малыми, чтобы обеспечить адекватность линейной модели. Затем определяются оценки b₁, b₂,…,b_к коэффициентов регрессии, строится линейная модель у=b₀х₀+b₁x₁+b₂x₂, проверяется ее адекватность и определяется направление градиента.

Дальнейшее движение по градиенту осуществляется переходом из точки х₁₀, х₂₀ в точку с координатами х`<sub>1</sub>=х<sub>10</sub>+b′<sub>1</sub>l, х`₂=х₂₀+b′₂l, где l - положительное число, определяющее величину шага в направлении градиента. Эта точка используется для планирования нового эксперимента. Вновь проводятся все те же действия, что и при предыдущем планировании и определяется новое направление градиента и переход на следующую точку. Таким же образом осуществляются последующие циклы поиска до тех пор, пока все координаты градиента (все оценки коэффициентов b_j) не окажутся весьма близкими к нулю. Подобная ситуация служит признаком того, что достигнута некоторая окрестность точки экстремума.

Рис. 5. Поиск максимума методами градиента (1)

и крутого восхождения (2)

Недостатком такого алгоритма реализации метода градиента является то, что он требует значительного числа опытов и не обладает высокой помехоустойчивостью.

Другой, часто используемой разновидностью градиентного метода является метод крутого восхождения (метод Бокса-Уилсона).

Процедура при реализации этого метода так же, как и в методе градиента, начинается с выбора начальной точки проведения эксперимента и определения направления градиента. Однако в дальнейшем после каждого шага определение градиента не производится, а производится процедура одномерного поиска, когда шаговое движение из начальной точки по направлению градиента осуществляется до попадания в частный оптимум по кривой 2 (см. рис.5). Практически это реализуется путем определения у(х₁х₂) после каждого шага: если функция отклика не уменьшается, то движение продолжается. Когда у(х₁х₂) начнет уменьшаться, движение по градиенту прекращается, проводится новое планирование для точки частного оптимума, принимаемой за исходный уровень. Проводятся опыты, и определяется новое направление движения, и так до достижения максимума целевой функции, когда все координаты градиента в очередном цикле будут близки к нулю.

Очевидно, что метод крутого восхождения по сравнению с градиентным методом обладает меньшей трудоемкостью.

Рекомендуемая литература

1. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. М.,1976

2. Боровиков В. STATISTICA. Искусство анализа данных на компьютере: Для профессионалов. 2-е изд..-СПб.: Питер, 2003.-688с.

3. ГОСТ 24026-80 «Исследовательские испытания. Планирование эксперимента. Термины и определения. М.,1980.

4. Грачев Ю. П. Математические методы планирования экспериментов. М.: Пищевая промышленность, 1979.

5. Джонсон Н. Лион Ф. Статистика и планирование эксперимента в технике и науке: Методы планирования эксперимента. – М.: Мир, 1981. – 520 с.

6. Злобин Л.А. Оптимизация технологических процессов хлебопекарного производства..- М.: Агропромиздат, 1987.- 200с.

7. Талантов В.Н., Матвеева И.В. Математическое моделирование технологических процессов хлебопекарного производства: Учебное пособие, МТИПП.-1991, 51с.

8. Тихомиров В.Б. Планирование и анализ эксперимента М.: Легкая индустрия, 1974.-262с.

9. Федоров В.В. Теория оптимальных экспериментов (при выяснении механизма явлений), М., 1971.

10. Фетисов Е.А. Статистические методы контроля качества молочной продукции: Справочное руководство, - М.: Агропромиздат, 1985. – 80с.