Условия отсутствия ударных реакций. Центр удара.
Сначала найдем условия, которые необходимы для того, чтобы при ударе не возникали ударные импульсы реакции. Примем, что ударные импульсы в точках А и В равны нулю, и найдем те ограничения, которые эти условия накладывают на остальные величины, входящие в уравнения (6.17) и (6.18) . Из этих уравнений получим:
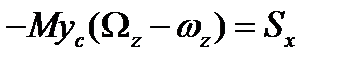
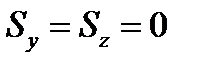
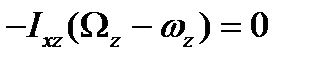 (6.19)
(6.19)
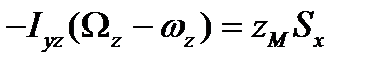
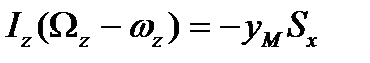
Из второго и третьего уравнений следует, что внешний ударный импульс должен иметь направление, параллельное оси ох, т. е. он должен быть перпендикулярен к плоскости, проведенной через ось вращения и центр масс тела. Для удобства дальнейших рассуждений введем новую систему координат 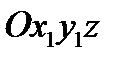 с осями, параллельными исходным осям, и с началом в точке О (рис 84), находящейся на оси вращения тела Оz, причем
с осями, параллельными исходным осям, и с началом в точке О (рис 84), находящейся на оси вращения тела Оz, причем 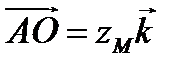 . В новой системе координат
. В новой системе координат 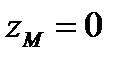 . В новой системе координат уравнения (6.19) сохраняют свой вид. Имея в виду условие
. В новой системе координат уравнения (6.19) сохраняют свой вид. Имея в виду условие 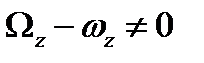 и
и 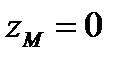 , получим
, получим 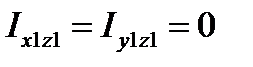 , т. е. ось вращения должна быть главной осью инерции для точки О. Из первого и последнего уравнения находим
, т. е. ось вращения должна быть главной осью инерции для точки О. Из первого и последнего уравнения находим
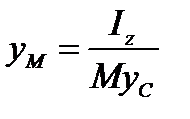 (6.20)
(6.20)
Здесь мы воспользовались тем, что 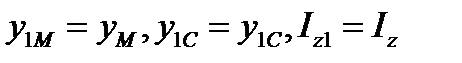 . Значит, линия действия импульса S должна отстоять от оси вращения на расстоянии, равном приведенной длине физического маятника (см. §5.гл 12).
. Значит, линия действия импульса S должна отстоять от оси вращения на расстоянии, равном приведенной длине физического маятника (см. §5.гл 12).
Таким образом, если удар не передается на опоры, то должны выполняться следующие условия:
1) линия действия ударного импульса должна быть перпендикулярна к плоскости, содержащей центр масс тела и ось вращения;
2) плоскость, содержащая ударный импульс и перпендикулярная к оси вращения, должна пересекаться с этой осью в точке, для которой ось вращения, является главной осью инерции;
3) линия действия ударного импульса должна отстоять от оси вращения на расстоянии, определяемом равенством (6.20).
Точка М в плоскости yAz (см. рис. 84), в которой приложен ударный импульс 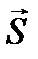 , удовлетворяющий всем указанным условиям, называется центром удара.
, удовлетворяющий всем указанным условиям, называется центром удара.
Следует отметить, что центр удара может и не существовать. Такая ситуация возникает, например, тогда, когда ни для одной из точек на оси вращения сама ось вращения не является главной осью инерции.
| С |
| цу |
| А |
| z |
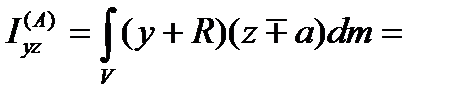
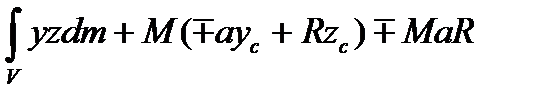 .
.
| цу |
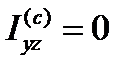 , второе слагаемое также равно нулю
, второе слагаемое также равно нулю 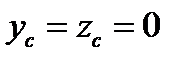 . Ось ОY направлена вниз и проходит через точки С и А. третье слагаемое равно нулю, если a=0, где a – расстояние от точки подвеса до оси ОY . Расстояние до центра удара определим по формуле (3.89)
. Ось ОY направлена вниз и проходит через точки С и А. третье слагаемое равно нулю, если a=0, где a – расстояние от точки подвеса до оси ОY . Расстояние до центра удара определим по формуле (3.89)
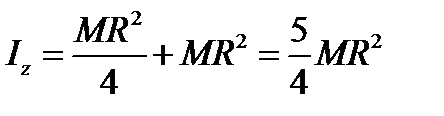 ,
, 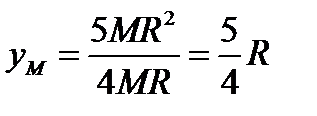 .
.
Дата добавления: 2019-12-09; просмотров: 778;











