Теоремы об изменении количества движения и кинетического момента при ударе.
Как указывалось в главе 10, формула 3.17, теорема об изменении главного вектора количества движения имела вид
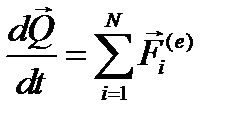 , (6.10)
, (6.10)
где 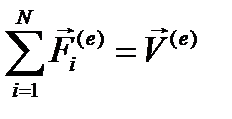 - главный вектор внешних сил, действующих на систему. Умножим обе части формулы (6.10) на
- главный вектор внешних сил, действующих на систему. Умножим обе части формулы (6.10) на 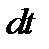 , тогда-
, тогда- 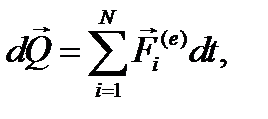 и проинтегрируем обе части, получим
и проинтегрируем обе части, получим
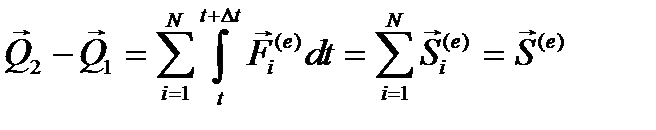 ,
,
здесь 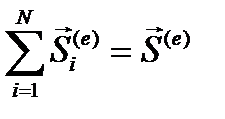 -главный импульс внешних сил. Вспоминая также, что
-главный импульс внешних сил. Вспоминая также, что 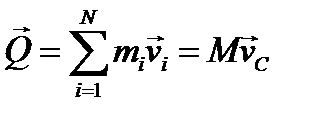 , получаем окончательную формулу изменения главного вектора количества движения при ударе
, получаем окончательную формулу изменения главного вектора количества движения при ударе
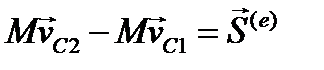 (6.11)
(6.11)
Теорема об изменении главного вектора момента количества движения или кинетического момента имела вид
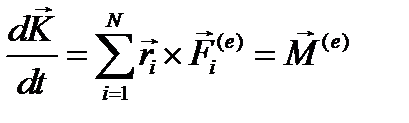 . (6.12)
. (6.12)
Так же как и выше умножим обе части формулы (6.12) на 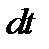 , тогда
, тогда 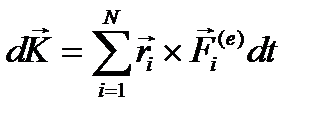 и проинтегрируем обе части, получим
и проинтегрируем обе части, получим
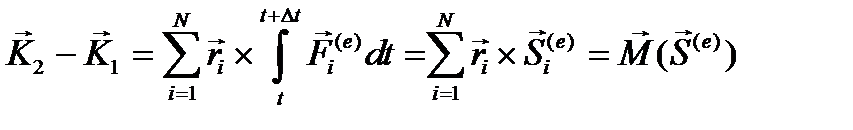 , (6.13)
, (6.13)
где 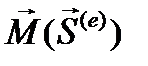 - главный момент импульсов внешних сил.
- главный момент импульсов внешних сил.
Запишем уравнения (6.13) в проекциях на оси координат. Для твердого тела в качестве осей координат удобнее выбрать оси, жестко связанные с телом; начало координатной системы следует выбрать либо в неподвижной точке О тела (если такая точка существует) либо в его центре масс С. Следует отметить, что при ударе все точки системы, в частности, твердого тела, не перемещаются. Поэтому можно выбрать любую систему координатных осей, жестко связанных с телом и заменить векторные уравнения (6.13) тремя скалярными уравнениями (см. глава 11, §2):
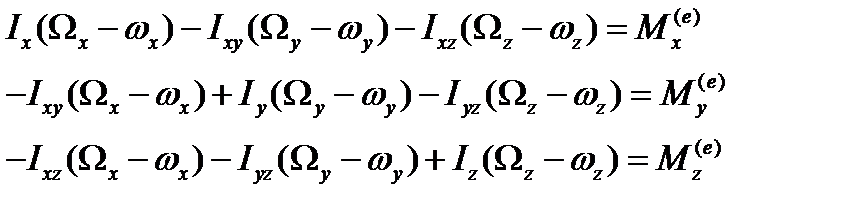 (6.14)
(6.14)
В этих уравнениях 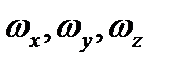 и
и 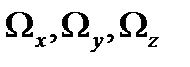 — проекции вектора угловой скорости тела в начале и конце удара,
— проекции вектора угловой скорости тела в начале и конце удара, 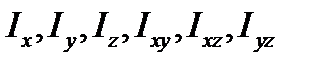 — соответствующие моменты инерции тела,
— соответствующие моменты инерции тела, 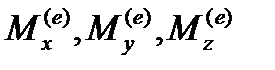 — проекции главного момента импульсов внешних ударных сил. Если за оси координат приняты главные оси инерции тела, то уравнения (6.14) примут такой вид:
— проекции главного момента импульсов внешних ударных сил. Если за оси координат приняты главные оси инерции тела, то уравнения (6.14) примут такой вид:
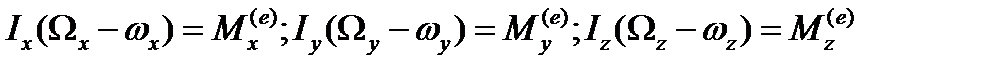 .
.
Дата добавления: 2019-12-09; просмотров: 759;











