Задача Герца о прямом и центральном ударе двух тел.

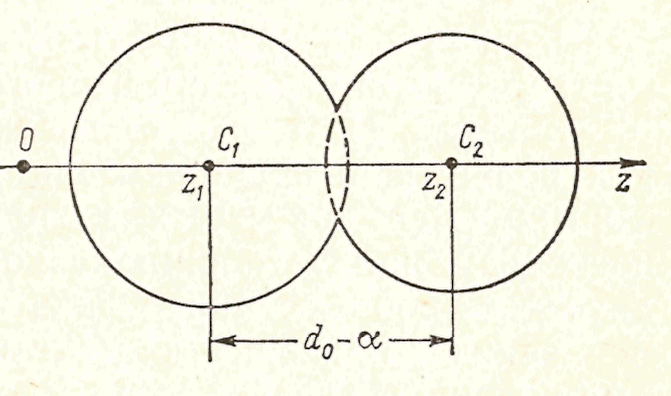
Соударение тел — это сложный процесс, определяющими факторами которого являются форма тела и скорость соударения. Наиболее простая и совершенная форма тела — шар. Поэтому из всех известных в настоящее время теорий удара самой простой и совершенной является теория Герца соударения шаров. Предположим, что до удара шары движутся поступательно со скоростями, направленными по прямой, соединяющей их центры. Будем считать, что эта прямая совпадает с неподвижной осью z (рис. 83), причем координата 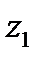центра масс первого шара всегда меньше координаты центра масс второго. 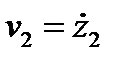Если скорость первого шара с радиусом больше скорости второго шара с радиусом 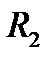, то в некоторый момент , когда шары коснутся друг друга в одной точке, произойдет соударение. Развивающуюся при ударе контактную силу P(t) называют ударной силой. В принятых обозначениях уравнения движения центров масс шаров имеют вид

.

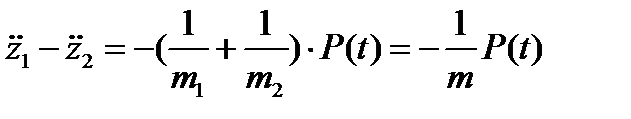
Отсюда

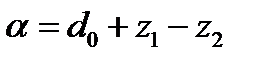
где 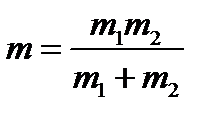— приведенная масса. Расстояние между центрами масс шаров при соударении равно 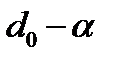, т.е. . Уравнение с учетом сказанного принимает вид

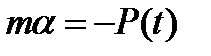(6.6)

Рис 83

Величину α, равную относительному смещению центров масс шаров, принято называть местным смятием. Термин «смятие» употребляется здесь не потому, что деформации предполагаются пластическими, а потому, что относительное перемещение шаров при силовом контакте происходит в основном вследствие дефор­мации (смятия) их в зоне контакта.

Задача о статическом сжатии шаров в рамках классической теории упругости была решена Герцем в 1881 г. Решение это очень красиво, но сложно. Полученное решение показывает, что деформации быстро затухают по мере удале­ния от места контакта. Установленная Герцем зависимость между контактной силой Р и смещением α имеет вид

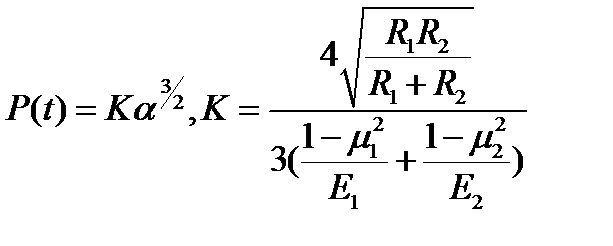(6.7)

здесь 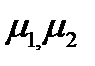- коэффициенты Пуассона, а и 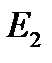-модули Юнга соответственно первого и второго шаров.

Формула (6.7), строго говоря, является приближенной, так как получена в предположении, что в зоне контакта шары де­формируются как плоские упругие полупространства. При скоростях соударения шаров, при которых еще не возникают пластические деформации, это условие выполняется. Таким образом, при упругом ударе шаров можно считать, что в уравнении (6.6) величины Р(t) и α связаны соотношением (6.7), т.е.

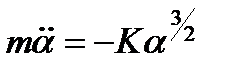(6.8)

Нелинейное уравнение (6.8), является уравнением вида , умножая левую и правую части на 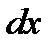, получим 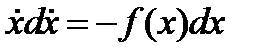- уравнение с разделяющимися переменными

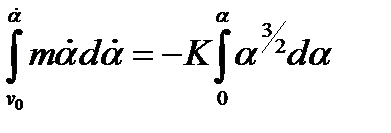
или

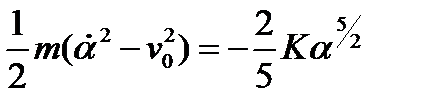(6.9)

В момент обращения скорости относительного смещения 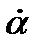в нуль величина α достигает максимального значения 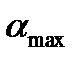, поэтому

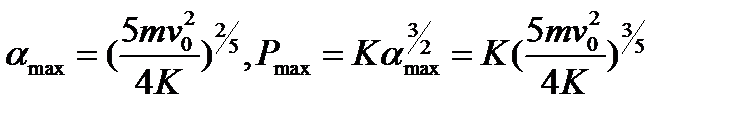
На первой стадии удара, когда величина α возрастает во времени, уравнение (6.9) можно записать в виде

.

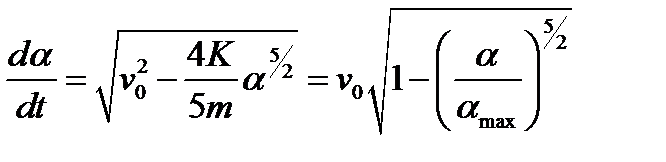Интегрируя его, получаем

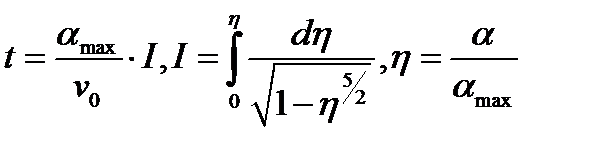
Зависимость t от η может быть найдена только путем численного интегрирования. Определенный же интеграл при η = 1 вычисляется аналитически І= 1,4716.

Время нарастания контактной силы P(t) равно времени ее спада, поэтому время соударения T, выражается через вычисленный интеграл І по формуле

Полагая, что соударяются два одинаковых стальных шара и , .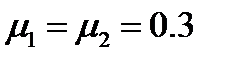

При R = 1 см (m = 32,7 г) и 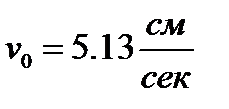получаем ,

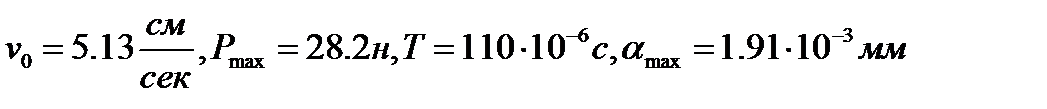Для сравнения проследим, как изменятся эти величины при увели­чении скорости в 10, а затем и в 100 раз. В первом случае имеем

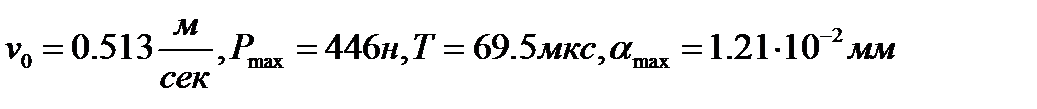
Во втором

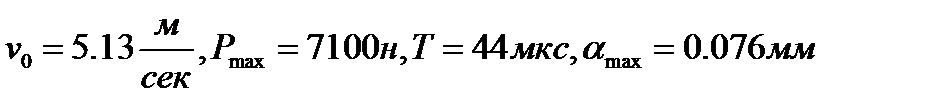
При больших скоростях теорию Герца используют только для приближенной оценки основных параметров удара, так как даже у закаленных шаров, изготовленных из высококачественной стали, при скоростях соударения примерно 5—8 м/с наблюдаются местные пластические деформации.