Динамические характеристики вынужденных колебаний.

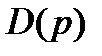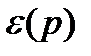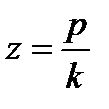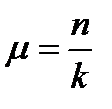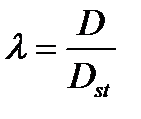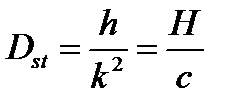Определим зависимость амплитуды вынужденных колебаний в функции от частоты вынужденных колебаний и фазу . Для этого введём безразмерные коэффициенты (коэффициент расстройки), (безразмерный коэффициент сопротивления) и коэффициент динамичности , где (отклонение системы от положения равновесия под действием постоянной силы H . Тогда, вынося 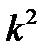из под корня в первой формуле (5.19), можно записать

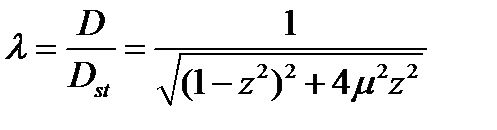
Рассматривая μ как параметр, построим график 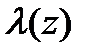. Сразу видно из приведённой формулы, что 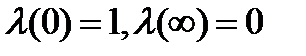, Обозначим подкоренное выражение в знаменателе как 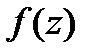, вычислим производную 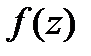по z и приравняем её нулю. Максимуму 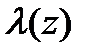соответствует минимум функции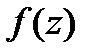

.

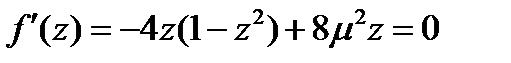Итак, есл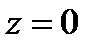и и 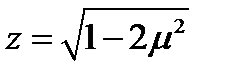, то функция 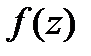имеет экстремум, причём второе значение имеет место лишь при 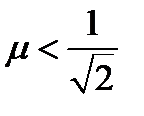. Зависимость 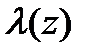, при различных значениях параметра μ , представлен на графике рис (74) ; для 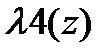параметр μ=0.707.

Рис 74

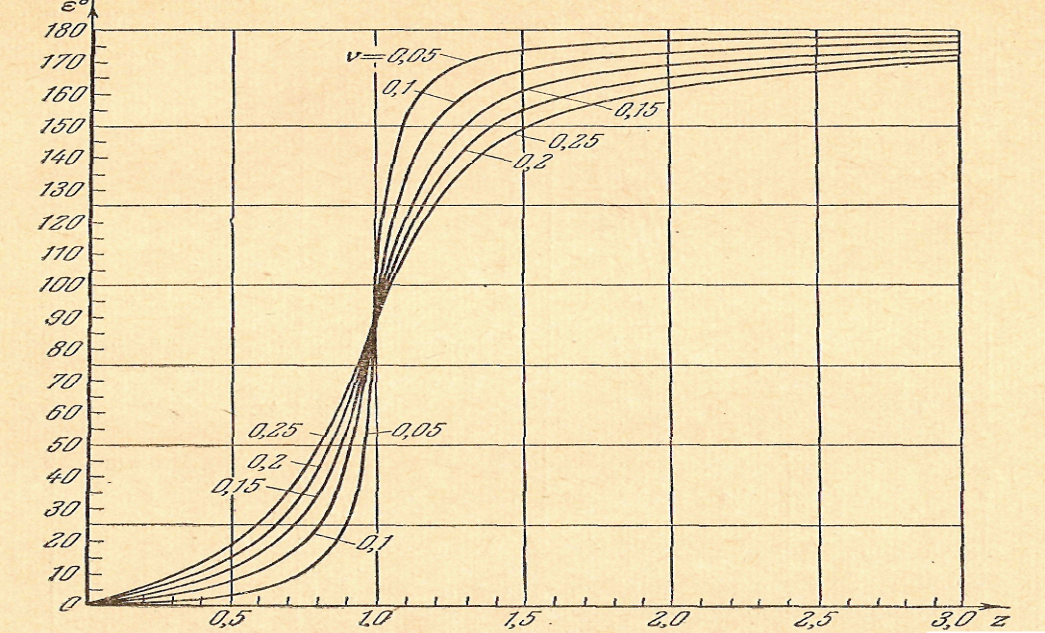
Для построения графика 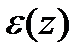преобразуем вторую формулу (5.19) к виду 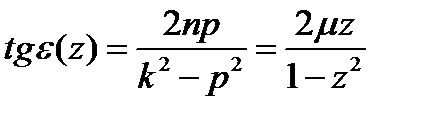. Зависимость 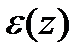, при различных

значениях параметра μ , представлен на графике (рис 75).

Рис 75

Глава 19.

Элементарная теория удара