Вывод уравнения Лагранжа второго рода.
Уравнения Лагранжа второго рода представляют дифференциальные уравнения несвободной системы, составленные в обобщенных координатах. Наибольшее распространение получили уравнения в независимых обобщенных координатах, — их обычно и называют уравнениями Лагранжа второго рода, а иногда просто уравнениями Лагранжа, так как уравнениями Лагранжа первого рода пользуются сравнительно редко. Рассмотрим систему с n степенями свободы, подчиненную идеальным голономным связям. Положение системы в пространстве будем определять n независимыми обобщенными координатами 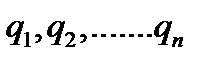 . Вектор-радиус
. Вектор-радиус 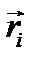 любой точки системы может быть выражен через обобщенные координаты и время
любой точки системы может быть выражен через обобщенные координаты и время 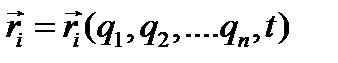 , а возможные перемещения определятся как вариации вектор-радиусов;
, а возможные перемещения определятся как вариации вектор-радиусов;
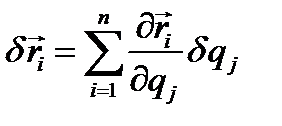 .
.
Так как все обобщённые координаты считаем независимыми, то все 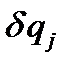 представляют произвольные бесконечно малые величины. Докажем предварительно два тождества Лагранжа. Составим выражения векторов скоростей точек системы:
представляют произвольные бесконечно малые величины. Докажем предварительно два тождества Лагранжа. Составим выражения векторов скоростей точек системы:
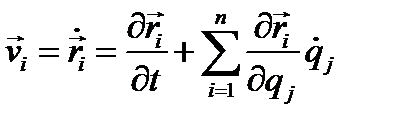 (4.19)
(4.19)
Производные обобщенных координат по времени, т. е. величины 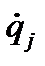 называются обобщенными скоростями. Формулы (4.19) показывают, что скорость
называются обобщенными скоростями. Формулы (4.19) показывают, что скорость 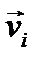 любой точки линейно выражается через обобщенные скорости, Поэтому, обозначая через к произвольный индекс, изменяющийся от 1 до n, будем иметь:
любой точки линейно выражается через обобщенные скорости, Поэтому, обозначая через к произвольный индекс, изменяющийся от 1 до n, будем иметь:
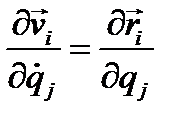 (4.20)
(4.20)
Это первое тождество Лагранжа. Докажем второе тождество
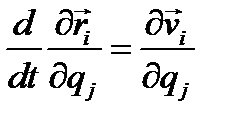 (4.21)
(4.21)
Для этого, дифференцируя обе части (4.19) по 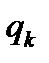 , получим
, получим
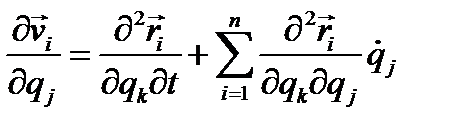
С другой стороны, составим непосредственно
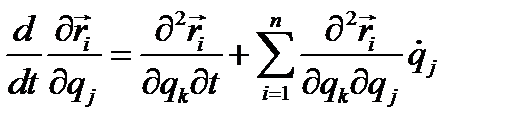
Сравнивая последние два равенства, убеждаемся в справедливости соотношения (4.21). Обратимся к общему уравнению динамики (4.18) и перепишем его в виде
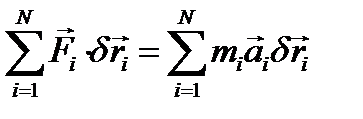 (4.22)
(4.22)
Первая сумма уже была выражена через обобщенные координаты (4.11); она равна 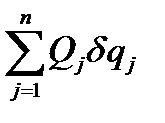 , где Qj — обобщенная сила. Что касается второй суммы в уравнении (4.22), то ее можно преобразовать, пользуясь (4.9) и меняя порядок суммирования:
, где Qj — обобщенная сила. Что касается второй суммы в уравнении (4.22), то ее можно преобразовать, пользуясь (4.9) и меняя порядок суммирования:
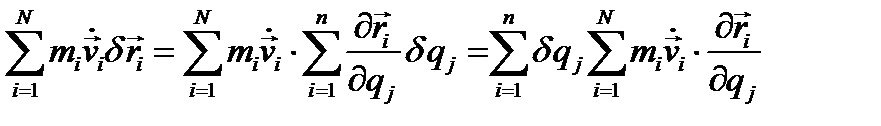 (4.23)
(4.23)
скалярное произведение под знаком суммы преобразуется к виду
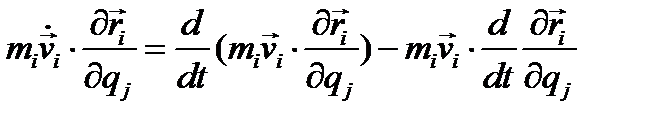
или по формулам (4.20) и (4.21)):
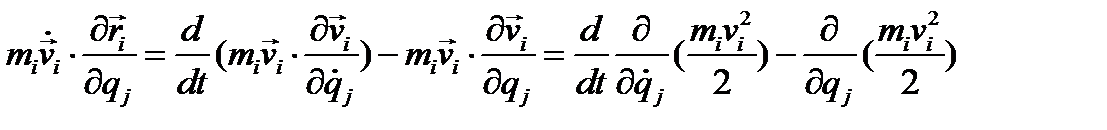
Подставляя последнее выражение в круглую скобку правой части равенства (4.23) и замечая, что сумма 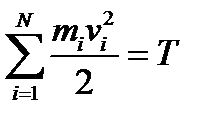 определяет кинетическую энергию системы, получим:
определяет кинетическую энергию системы, получим:
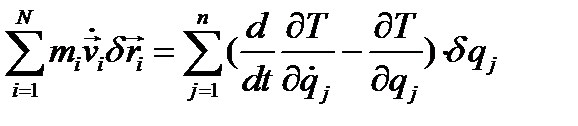
Уравнение (4.18) теперь перепишется так:
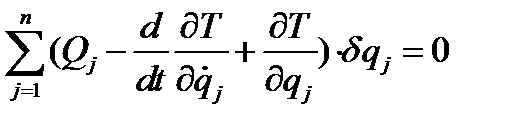 (4.24)
(4.24)
Последнее равенство может выполняться при произвольных 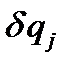 , только если все круглые скобки равны нулю. Таким образом, мы приходим к уравнениям Лагранжа второго рода, составленным в независимых обобщенных координатах для системы с голономными связями:
, только если все круглые скобки равны нулю. Таким образом, мы приходим к уравнениям Лагранжа второго рода, составленным в независимых обобщенных координатах для системы с голономными связями:
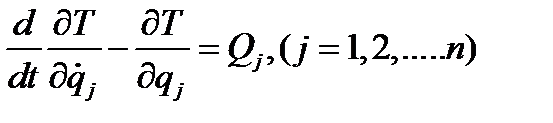 (4.25)
(4.25)
Уравнения (4.25) представляют совокупность n (по числу степеней свободы) обыкновенных дифференциальных уравнений второго порядка с n независимыми обобщенными координатами, являющимися искомыми функциями времени. Оператор
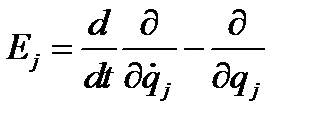 (4.26)
(4.26)
носит название оператор Эйлера-Лагранжа. Уравнению Лагранжа второго рода можно дать и другое доказательство. Как указывалось выше, положение любой точки можно представить в виде 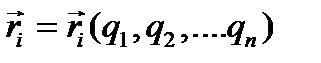 , где n - число независимых обобщённых координат, равное, в нашем случае, числу степеней свободы системы. Тогда
, где n - число независимых обобщённых координат, равное, в нашем случае, числу степеней свободы системы. Тогда 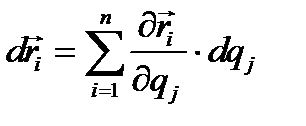 и величину
и величину 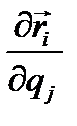 можно представить как направление вдоль координатной линии
можно представить как направление вдоль координатной линии 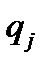 . Спроектируем основное уравнение динамики точки на это направление
. Спроектируем основное уравнение динамики точки на это направление
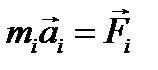
(при этом 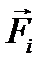 есть сумма всех сил: внешних и внутренних, действующих на точку) и сложим все полученные проекции.
есть сумма всех сил: внешних и внутренних, действующих на точку) и сложим все полученные проекции.
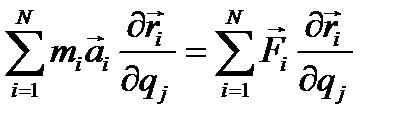 (4.27)
(4.27)
Справа в выражении (4.27) стоит по (4.11) обобщённая сила, а слева выражение (4.23). Проведя аналогичные преобразования, получаем уравнение Лагранжа второго рода.
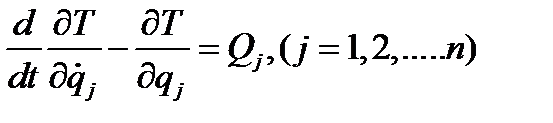 .
.
Пример. Рассмотрим задачу о колебаниях стержня массы m и длины l, подвешенного в точке D к вращающемуся вокруг вертикальной оси АВ стержню АВD. Момент инерции стержня АВD равен J. За обобщённые координаты выберем углы 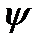 и φ. Кинетическая энергия системы в общем виде запишется в форме
и φ. Кинетическая энергия системы в общем виде запишется в форме
| М |
| φ |
| mg |
| l |
| a |
| ψ |
| z |
| y |
| x |
| А |
| В |
| С |
| D |
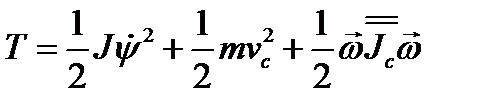 ,
,
Здесь 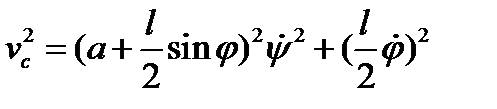 - скорость центра стержня,
- скорость центра стержня, 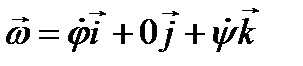 - вектор угловой скорости стержня,
- вектор угловой скорости стержня, 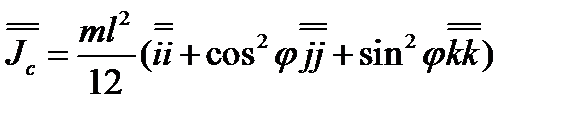 -тензор инерции стержня относительно центра С. Подставив введённые обозначения в формулу для кинетической энергии, получим
-тензор инерции стержня относительно центра С. Подставив введённые обозначения в формулу для кинетической энергии, получим
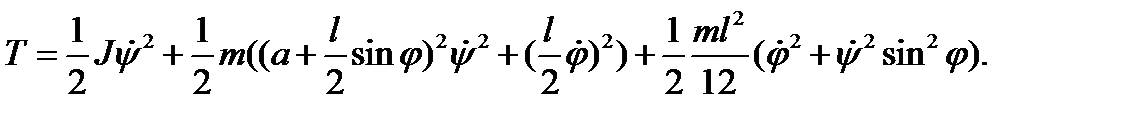
Проведя несложные преобразования, запишем кинетическую энергию в виде
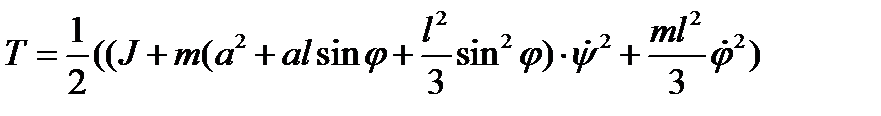
Совсем нетрудно получить и выражение для возможной работы сил--момента 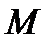 и силы тяжести
и силы тяжести 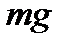 .
.
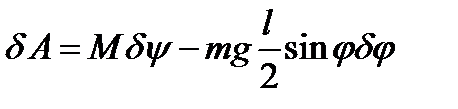 .
.
Обобщённые силы будут 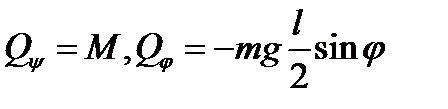 . Составим уравнения движения с помощью уравнения Лагранжа второго рода:
. Составим уравнения движения с помощью уравнения Лагранжа второго рода:
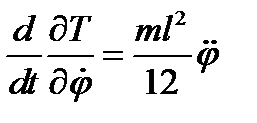 ; обозначим
; обозначим 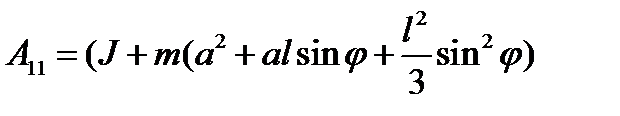 , и
, и 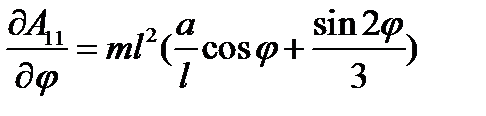 , тогда
, тогда 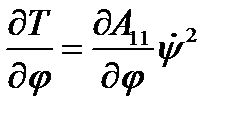 и первое уравнение имеет вид
и первое уравнение имеет вид
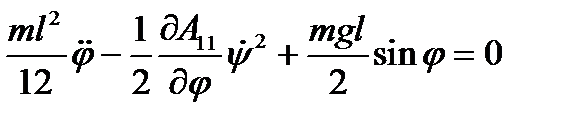 .
.
Второе уравнение будет
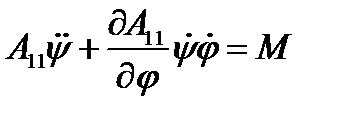 .
.
Дата добавления: 2019-12-09; просмотров: 760;











