Принцип освобождаемости. Идеальные связи.

Ограничивая свободу движения системы, связи действуют на точки системы посредством сил, называемых реакциями связей. Чтобы не смешивать реакции связей с остальными силами, при­ложенными к точкам несвободной системы, назовем эти последние силы условно задаваемыми

Можно сказать, что задаваемыми силами являются те из сил, приложенных к системе, которые сохра­няются, если связи мгновенно, исчезнут или, как иногда говорят, «ослабнут». Прикладывая к точкам 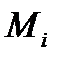системы с массами 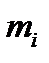наряду с равно­действующей 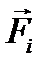задаваемых сил равнодействующую реакций свя­зей 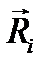составим уравнения движения системы точек:

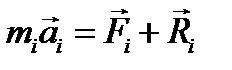. (4.5)

Эти уравнения показывают, что несвобод­ную систему точек можно рассматривать как свободную, дви­жущуюся под действием задаваемых сил и реакций связей. Использование этого положения, именуемого принципом освобо­ждаемости, успешно применялся в статике твердого тела, заменяя опоры их реак­циями. В свете учения о связях смысл принципа освобождаемости ста­новится более ясным. Применяя принцип освобождаемости, мы мысленно отбрасываем связи, заменяя их действие динамически эквивалентным действием реакций связей. При этом число степеней свободы системы увеличивается и расширяется многообразие воз­можных перемещений. Поясним это на следующем простом примере. Тяжелая балка, лежащая на двух опорах (считаем связь удержи­вающей), не имеет свободы перемещения. Откидывая одну из опор и прикладывая к балке соответствующую опорную реакцию, мы этим не нарушаем равновесия балки, но балка получает свободу пере­мещения вращения вокруг оставшейся опоры - и может уже рас­сматриваться как система с одной степенью свободы. Принцип освобождаемости позволяет переводить реакции связей в класс задаваемых сил, что может оказаться полезным при прове­дении некоторых рассуждений. В случае идеально гладкой поверхности реакция целиком сво­дится к силе, нормальной к поверхности. Таким образом, если связью служит поверхность без трения, то реакция связи нормальна к связи. В этом случае элементарная работа реакции на любом возможном перемещении точки равна нулю, так как сила напра­влена перпендикулярно к перемещению. В действительности не существует ни абсолютно гладких, ни абсолютно твердых тел, так что работа реакций на любом возмож­ном перемещении отлична от нуля. Но, с другой стороны, во мно­гих практических случаях в первом приближении можно или прене­бречь работой сил трения и говорить о «практически» гладких поверхностях, или считать силу трения как заданную силу. Тот факт, что на практике постоянно приходилось встречаться со связями, сумма работ реакций которых на любом возможном перемещении системы может быть в допустимом приближении при­нята равной нулю, привел к установлению важной механической абстракции идеальных связей.

Идеальными связями называются такие связи, сумма элемен­тарных работ реакций которых на любом возможном переме­щении системы равна нулю. Тогда условие идеальности связей будет, по предыдущему, заключаться в равенстве нулю элементарной работы 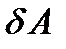реакций связей на возможном перемещении

(4.6)