Статический принцип возможных перемещений.

Статический принцип возможных перемещений формулируется так: необходимое и достаточное условие равновесия системы, под­чиненной стационарным, идеальным, двухсторонним, голономным связям,- заключается в равен­стве нулю суммы элементарных работ задаваемых сил на любом возможном перемещении системы из рассматриваемого положения равновесия.

Обозначим через 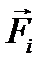равнодействующую задаваемых сил, прило­женных к какой-нибудь точке 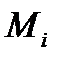системы, через 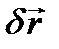возможное перемещение этой точки и через 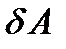сумму элементарных работ задаваемых сил на возможном перемещении системы. Тогда анали­тическое выражение принципа возможных перемещений будет иметь вид:

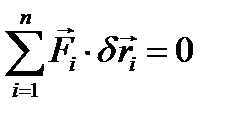(4.7)

Чтобы доказать необходимость принципа, предположим что несвободная система, подчиненная стационарным связям, находится в положении равновесия. Тогда каждая ее точка находится в равно­весии и, по принципу освобождаемости, равнодействующая заданных сил 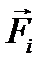и реакций связи 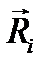, приложенная к какой-либо точке 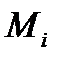должна быть равна нулю. Равна нулю будет и работа этой равно­действующей, так что

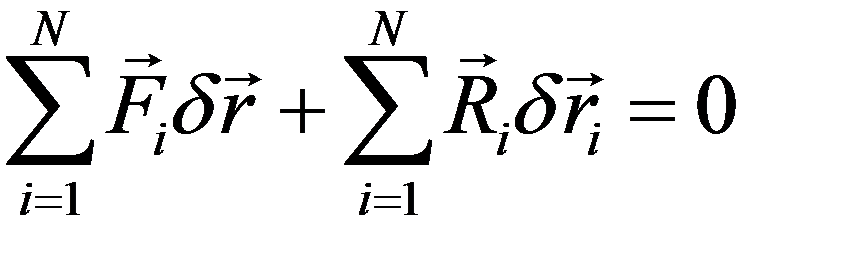
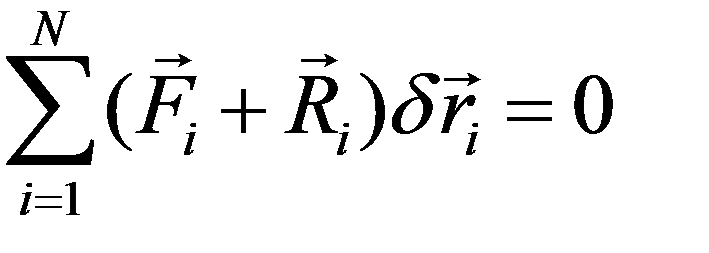
или

но вторая сумма равна нулю по условию идеальности связей; сле­довательно, необходимость принципа доказана.

Для доказательства достаточности принципа, т. е. существова­ния равновесия при выполнении условия (4.7), рассуждение ведется от обратного. Предположим, что условие (4.7) выполнено, а система в рассматриваемом положении все же не находится в равновесии. Тогда система, если в начальный момент представить себе ее покоя­щейся, под действием задаваемых сил и реакций связи придет в дви­жение и за малый промежуток времени совершит некоторое дейст­вительное перемещение, входящее в случае стационарных связей в число возможных. Тогда возможная кинетическая энергия 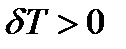и при этом будет совершена положитель­ная работа 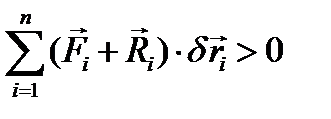. Разбивая на две суммы, получим:

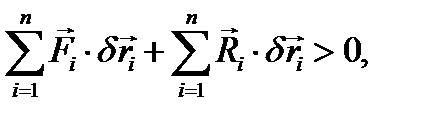
но вторая сумма по условию идеальности связей равна нулю, сле­довательно,

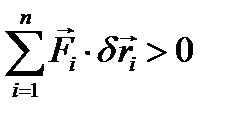
что противоречит принятому предположению (4.7), что и требовалось доказать. Можно показать, что необходимым и достаточным условием равновесия системы сил являются хорошо известные из статики соотношения. Действительно

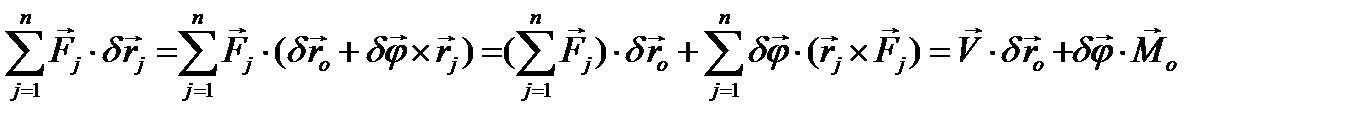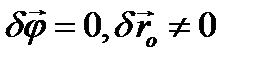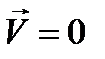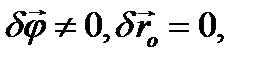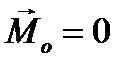Тогда среди возможных конфигураций системы можно всегда выбрать такие, что , тогда должно быть , а если то : необходимым и достаточным условием равновесия является равенство нулю главного вектора и главного момента системы сил

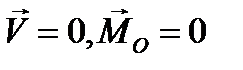(4.8)

Если задаваемые силы 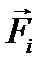консервативны, т. е. существует потен­циальная энергия П = П 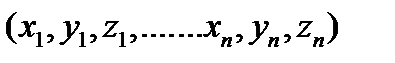, то

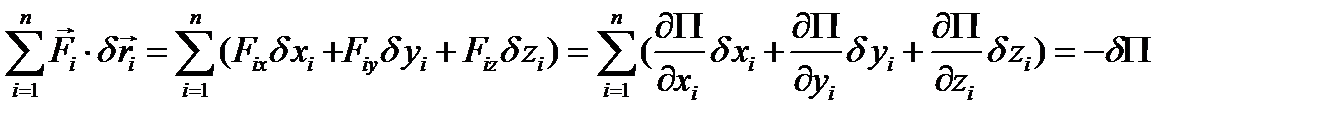
при этом выражение принципа возможных перемещений (3.7) приве­дется к равенству

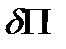=0,

выражающему необходимое условие экстремальности потенциаль­ной энергии в положении равновесия системы. Следовательно, из принципа возможных перемещений вытекает, что необходимые и достаточные условия равновесия несвободной системы с идеаль­ными связями под действием консервативных задаваемых сил совпадают с необходимым (но не достаточным) условием экстре­мума потенциальной энергии.

Составим выражение статического принципа возможных перемещений в обобщённых координатах. Вектор-радиус 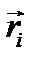любой точки системы может быть выражен через обобщенные координаты по формулам 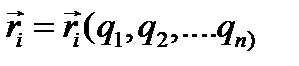, возможные перемещения определятся как вариации вектор-ради­усов

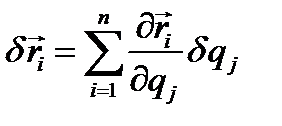(4.9)

Тогда работа сил на возможных перемещениях запишется в виде

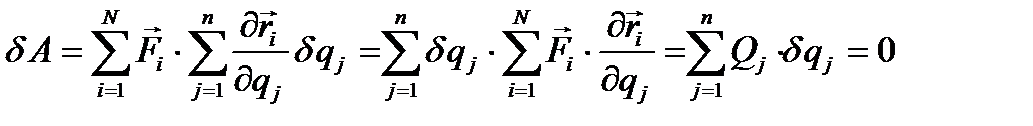, (4.10)

где 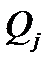представляет выражение

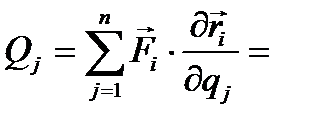
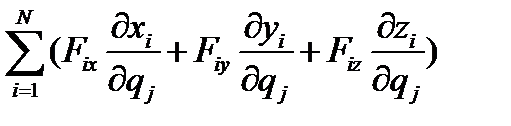(4.11)

называемое обобщённой силой. Для нахождения обобщённой силы, надо составить выражение возможной работы в обобщённых координатах; полученные коэффициенты при возможных перемещениях 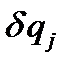и есть соответствующие этим координатам обобщённые силы. Если задаваемые силы 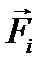консервативны, то, выразив предварительно потенциальную энергию через обобщённые координаты, по (4.9) получим

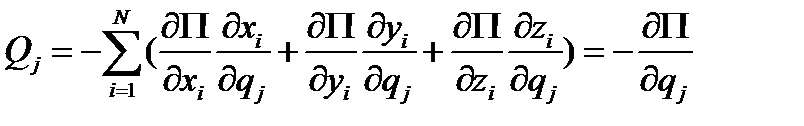(4.12)

Если обобщённые координаты выбраны независимыми, то обобщённые возможные перемещения 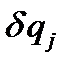в числе, равном числу степеней свободы, будут произвольны. Тогда из равенства (4.10) следует, что все коэффициенты при произвольных величинах 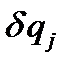должны по отдельности быть равными нулю:

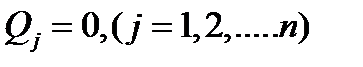(4.13)

Итак, необходимое и достаточное условие равновесия несвободной системы с голономными, идеальными, стационарными, двухсторонними связями заключается в равенстве нулю всех соответствующих независимым обобщённым координатам обобщённых сил в рассматриваемом положении равновесия системы. Полагая в этом случае, что потенциальная энергия П задаваемых сил также выражена через обобщённые координаты, будем иметь по (4.12) и (4.13) условия равновесия системы в виде

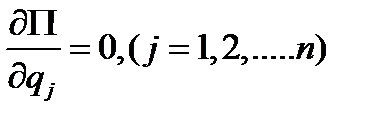. (4.14)

Эти равенства выражают необходимое условие экстремума потенциальной энергии в положении равновесия системы.

Рассмотрим пример: определить соотношение между моментом М0 и силой Q, если угол ОВА равен α, а угол ВОА - β. ОА=L.

Дадим системе возможное перемещение 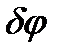по направлению момента и 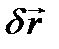против направления силы Q, тогда, согласно статическому принципу возможных перемещений, имеем

.

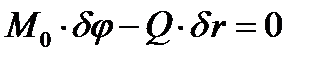O

A

B

Q

M0

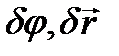Шатун АВ совершает плоско-параллельное движение, и для получения зависимости между можно применить два способа: первый- проекции перемещений концов отрезка на направление отрезка равны, следовательно

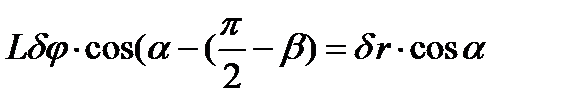или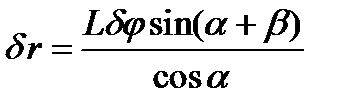

Подставляя полученное равенство в основное уравнение, получаем

.

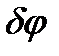
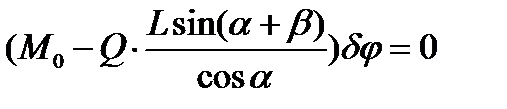Так как любое возможное перемещение, то

.

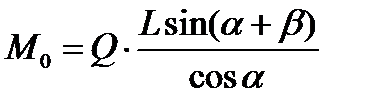Второй способ – использование определении мгновенного центра скоростей (мцс). В нашем примере (мцс) находится на пересечении продолжения отрезка ОА и перпендикуляра к ОВ, проведённого из точки В (пусть мцс находится в точке Р). Если обозначить через 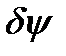поворот относительно мцс, то можно записать 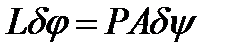и 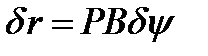, откуда следует 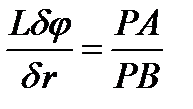. По теореме синусов из треугольника ОАВ имеем 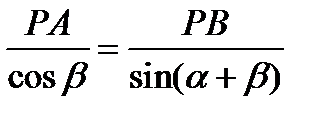или 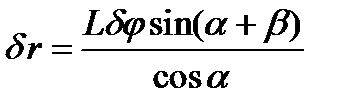. Получаем тот же результат.