Представление кинетической энергии как функции обобщённых скоростей.

Докажем, что кинетическая энергия является квадратичной функцией обобщенных скоростей. Для этого заметим

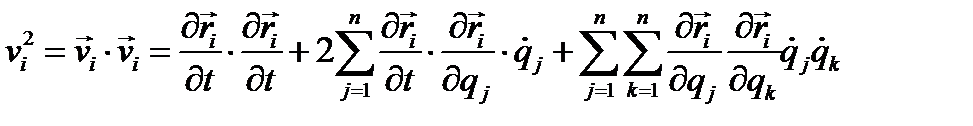
и полная кинетическая энергия будет равна

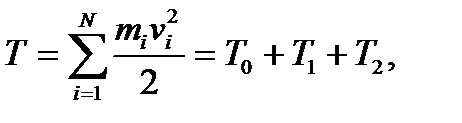(4.34)

где 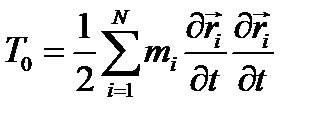- функция нулевой степени относительно обобщенных ско­ростей, 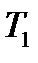- линейная функция обобщенных скоростей 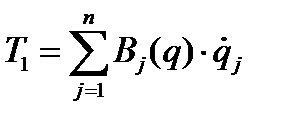, где обозначено 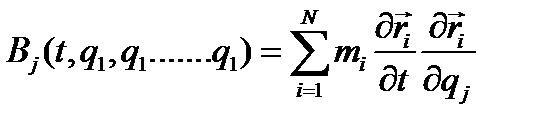, наконец, 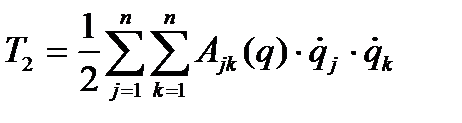, - функция второй степени от обобщенных скоростей, где .

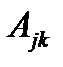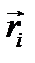Из определения функций следует, что ; величины с двумя индексами, обладающие таким свойством, называют сим­метричными. Если связи стационарны, то не зависит явно от времени; тогда, очевидно,

,

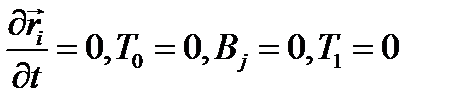и выражение кинетической энергии сводится к квадратичной форме от обобщённых скоростей, коэффициенты которой зависят от обобщённых координат.

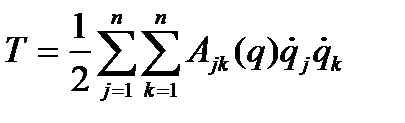(4.35)

Интеграл энергии.

Предположим, что время не входит явно в выражение кинетического потенциала (функции Лагранжа) 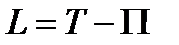, т.е. связи предполагаются стационарными. Составим полную производную по времени от кинетического потенциала, учитывая, что 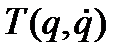, а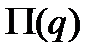

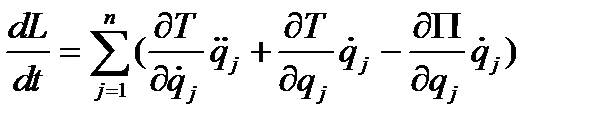(4.36)

Преобразуем первую сумму к виду

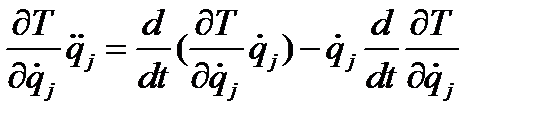, (4.37)

а уравнение Лагранжа запишем с учетом диссипации энергии и других сил в следующей форме

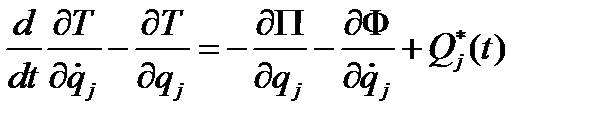. (4.38)

Подставив (4.37) в выражение (4.36), получим

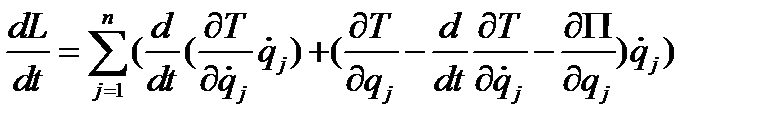. (4.39)

Сравнивая второе слагаемое в выражении (4.39) с уравнением Лагранжа в форме (4.38), перепишем полученное равенство (4.39) в виде

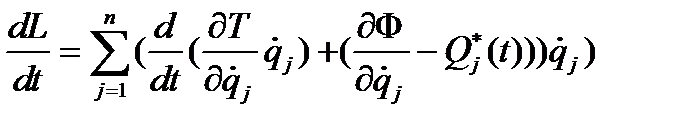. (4.40)

В случае стационарных связей 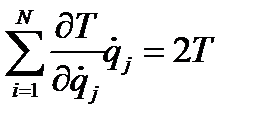, а (по формуле 4.32) , тогда выражение (4.40) можно записать в виде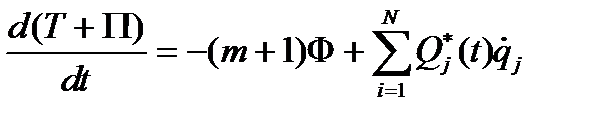

или 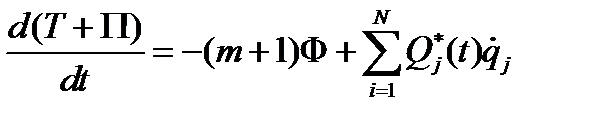. (4.41)

Изменение полной механической энергии, подчинённой стационарным связям, в единицу времени равно мощности непотенциальных приложенных сил (первое слагаемое в правой части (4.41) - мощность диссипативных сил).

Вопросы для самопроверки.

1. Напишите диф. уравнение движения стержня, скользящего концами по наклонной и горизонтальной поверхностям. Масса стержня m, длина l. Трение отсутствует (рис 1).

2. Что такое возможные перемещения (определение)?

Рис 1.

3. Сколько степеней свободы имеет система, состоящая из 4 (3,5…) точек, на которую наложено 4 (3,5…) голономных связей?

4. Что Вы можете сказать о связи, представленной выражением F= bx +cy -аt >0?

5. Сформулируйте статический принцип возможных перемещений (в самой общей формулировке).

6. Как формулируется статический принцип возможных перемещений в обобщенных координатах?

7. Как формулируется динамический принцип возможных перемещений (общее уравнение динамики)?

8. Как записывается уравнение Лагранжа 2го рода в случае консервативной системы сил?

9. Как записывается диссипативная функция Рэлея?

10. Напишите уравнение Лагранжа с учетом сил диссипации и возмущающих сил.

11. Как изменяется полная механическая энергия при наличии диссипации и возмущающих сил .

O

P

A

B

M

K

12. Определите горизонтальную реакцию в шарнире О, если угол ОАВ равен 120 град., точка К посе редине ОА, ОА=АВ=L.

O

A

B

Q

M0

13. Определить соотношение между моментом М и силой Q, если угол ОВА равен 30, а угол ВОА—60град.

14. Чему равна горизонтальная (вертикальная) реакция в шарнире В? Система состоит из двух стержней, в точке С шарнир, треугольник АВС равносторонний со сторонами АС=ВС=L, сила Р перпендикулярна ВС и приложена в середине стержня.

А

В

С

М

Р

РАЗДЕЛ ПЯТЫЙ