Аналитическая маршрутная фототриангуляциа

Следует сказать, что технологий ее выполнения довольно много. Рассмотрим те, что были предложенные в свое время Советскими фотограмметристами и хорошо раскрывают суть дела. Речь идет о способах частично зависимых моделей, независимых моделей и связок.

Сущность способа частично зависимых моделей в том, что вначале строится модель по первой стереопаре. За начало фотограмметрической системы координат принимается центр проекции левого снимка. Его угловые элементы внешнего ориентирования и базис фотографирования устанавливаются произвольно. Затем строится модель по второй стереопаре. Но за угловые элементы внешнего ориентирования ее левого снимка принимаются величины, которые характеризуют его положение относительно фотограмметрической системы координат используемой для построения первой модели. Так поступают с третьей и всеми последующими моделями. Зависимость в результате состоит в том, что оси фотограмметрических координат всех моделей оказываются взаимно параллельными.

Алгоритм решения задачи может быть сконструирован следующим образом. Предположим, что построение любой модели в маршруте осуществляется поворотом, как левого, так и правого снимков. Тогда при решении задачи задействованы следующие величины:

-угловые элементы внешнего ориентирования левого снимка a_л w_л k_л,, они известны;

_-элементы взаимного ориентирования a_л^¢ и k_л¢, характеризующие поворот левого снимка при построении модели, но с другой стороны, тоже являющиеся угловыми элементами внешнего ориентирования левого снимка, но относительно базисной системы координат. Они вычисляются в процессе взаимного ориентирования.

-элементы взаимного ориентирования a_п^¢ w¢_п и k_п¢ характеризующие поворот правого снимка, но являющиеся и его угловыми элементами внешнего ориентирования в базисной системе координат;

-элементы внешнего ориентирования правого снимка a_п w_п и k_п. относительно той же системы фотограмметрических координат, что и a_л w_л k_л. Их и нужно вычислить, для построения следующей модели.

Обозначим матрицы направляющих косинусов, соответствующие указанным выше системам угловых элементов внешнего ориентирования через A_л, A_Л, A_П и A_п.Таким образом матрица A_п – искомая. Очевидно, что каждой системе угловых элементов внешнего ориентирования отвечает система уравнений связывающих фотокоординаты точек на снимке с их пространственными координатами. Эти уравнения известны. Они имеют вид:

, , ,

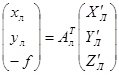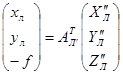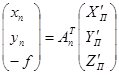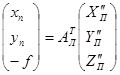
Из этих соотношений сразу же следует, что

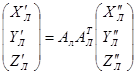и

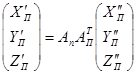
Координаты пары соответственных точек (X_Л¢ Y_Л¢ Z_Л¢ и X_П¢ Y_П¢ Z_П¢), а также (X_Л^² Y_Л^² Z_Л^² и X_П^² Y_П^² Z_П^²) определяются в разных системах, но их оси параллельны, то есть преобразование происходит из параллельных систем в параллельные, поэтому: 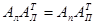, или

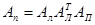
Возможно, формула будет понятнее, если поменять нижние индексы

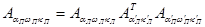
Для вычисления нужны, кроме того, углы наклона базиса n и t. Поскольку это углы, характеризующие поворот базисной системы координат относительно системы, используемой в дальнейшем для определения координат точек модели (т.е. которой соответствуют угловые элементы a_л w_л k_л), можно сразу же написать:

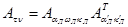
Используя эти углы и произвольно выбранное значение базиса фотографирования, можно вычислить его составляющие и координаты центра проекции правого снимка (формулы известны).

Итак, алгоритм рассматриваемого способа можно представить следующим образом:

- Измерение стереопары;

- Определение элементов взаимного ориентирования;

- Вычисление углов n и t, базисных составляющих и координат центра проекции правого снимка;

- Аналитическое трансформирование снимков стереопары относительно плоскости X_л^¢Y_л^¢;

^- Вычисление координат точек модели. При этом заметим, что X₀=B_Z, Z₀=B_Z , и после трансформирования снимков X^¢=x^о, Y¢=y^о, Z¢=-f, поэтому, скаляр N, используемый при решении прямой пространственной фотограмметрической засечки (при определении приращений координат точек модели) можно вычислять по формуле:

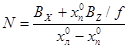
- Все выше указанное выполняют с каждой стереопарой маршрута. Масштаб последующей модели приводят к масштабу предыдущей с помощью масштабного коэффициента, который определяют по расстояниям от центров проекций S_П предыдущей стереопары и S_Л - последующей до связующих точек (точек выбранных в процессе построения и измерения модели в зоне тройного перекрытия снимков). Обычно используют несколько расстояний, и коэффициент вычисляют, как среднее весовое.

- Внешнее ориентирование построенной общей для всего маршрута модели.

В способе независимых моделей модели независимы между собой. Для их построения выбирают базисы произвольной длины, измеряют координаты соответственных точек, включенных в сеть, вычисляют элементы взаимного ориентирования в базисной системе координат и трансформируют снимки относительно плоскости, перпендикулярной к главной базисной плоскости левого снимка. В результате координаты точек модели можно вычислять по формулам нормального случая съемки. Как видим, данный вариант не требует вычисления элементов внешнего ориентирования снимков. Для построения общей для всего маршрута модели выполняют операцию внешнего ориентирования второй модели по отношению к первой, третьей по отношению к первым двум и т.д. Затем выполняют внешнее ориентирование общей модели.

В способе связок для каждой точки, включенной в фотограмметрическую сеть, составляются два уравнения коллинеарности (35), связывающие ее фотокоординаты x иy с пространственными координатами X,Y,Z соответствующей точки местности. Каждое из уравнений содержит 6 неизвестных, если они составлены для опознака (неизвестными являются элементы внешнего ориентирования снимка), и 9 неизвестных для точки, пространственные координаты которой подлежат определению. Фотокоординаты точек измеряют на всех снимках маршрута, после чего приступают к вычислению искомых координат, действуя в последовательности (которая уже неоднократно обсуждалась):

- Выбирают приближенные значения элементов внешнего ориентирования и искомых координат; Их находят, используя материалы аэрофотосъемки, старые карты, фотопланы и другие источники.

- Подставляют выбранные величины в уравнения коллинеарности. В результате получают фотокоординаты x_в, y_в, которые не будут равны измеренным и из-за погрешностей измерений и из-за неточности принятых приближенных величин.

- Составляют уравнения поправок, коэффициенты которых будут частными производными фотокоординат по соответствующим неизвестным. Разности между вычисленными и измеренными фотокоординатами – их свободные члены. Перед вычислением свободных членов в измеренные координаты вводят поправки за влияние различных факторов. Если m – число точек в сети, n – число снимков и k.-.число определяемых точек, то получим 2m уравнений, с 6n+k неизвестными.

- Составляют и решают нормальные уравнения, и полученные в результате поправки вводят в принятые значения неизвестных величин, то есть получают второе приближение.

- Используя исправленные значения, опять составляют уравнения поправок, затем нормальные уравнения и решают их. Таким образом, задача определения координат точек сгущения решается методом итераций, которые прерываются, либо в случае, когда очередные поправки окажутся пренебрежимо малы, либо по установленному максимальному числу итераций, если решение оказывается некорректным и нужно искать ошибки в исходных данных.

Этот способ дает возможность при построении сети использовать зафиксированные в полете элементы внешнего ориентирования (GPS определения, показания статоскопа, радиовысотомера и т.д.). Уравнивание, в этом случае, выполняют с учетом весов всех измеренных величин. Следует заметить, что он в настоящее время и наиболее популярен, так как практически нет ограничений на использование памяти ЭВМ, что ранее было серьезной проблемой.