Аналитическая аппроксимация и универсальный метод определения расчетных гидрометеорологических характеристик
При выполнении гидрологических расчетов в ходе проектирования мостовых переходов возникает необходимость в интерполяции и экстраполяции зависимостей гидрометеорологических величин, устанавливаемых по натурным данным.
Речь идет об аппроксимации гидрометеорологических зависимостей следующих типов:
1. Кривых связи расходов, уровней, осадков и т.д.
2. Кривых зависимости Н = f(Q), I = f(Н), V = f(Н) и других гидрометрических зависимостей.
3. Кривых вероятностей расходов, уровней, осадков, толщин снега и льда и т.д.
В настоящее время в практике проектирования наибольшее распространение получили графическая и некоторые другие разновидности графоаналитической аппроксимации. Всем им, однако, присущ один общий недостаток - субъективизм ручной аппроксимации, приводящий при одних и тех же исходных данных к неоднозначности решений, нередко выходящих за пределы разумного (например, на мостовом переходе через р. Хопер у ст. Усть-Бузулукская).
Универсальный метод аппроксимации гидрометеорологических величин, основанный на использовании метода «наименьших квадратов», состоит в следующем.
Для зависимостей 1-го и 2-го типов предполагается обязательное установление наличия либо отсутствия связи двух величин (X и Y) путем вычисления коэффициента корреляции. При положительном результате определяются аппроксимирующие функции и вычисляются значения Y = f(X) и X = f(Y) по заданию пользователя.
Особенностью вычисления кривых вероятности (зависимости 3-го типа) является то, что в качестве характеристик натурных точек задают только их ординаты (максимальные расходы, уровни, осадки, толщины снега или льда и т.д.), обычно в наблюденной последовательности. В процессе счета значения величин ранжируются в убывающем порядке. Для каждого члена ряда вычисляется его эмпирическая вероятность превышения по формуле (16.1) и строится аппроксимирующая зависимость Y = f(Рэ%) в масштабе клетчатки нормального распределения. Методика аналитической аппроксимации была разработана Г.А. Федотовым и Г.Г. Наумовым в 1984 году и реализована в виде программы «Гима-2» для компьютеров типа ЕС (Федотов Г.А., Наумов Г.Г. Применение программы Гима-2 при аналитической аппроксимации гидрометеорологических зависимостей. - М.: МАДИ, 1985. - 39 с), а затем в виде программы «Gist» для современных персональных компьютеров.
Неравномерная шкала по оси абсцисс строится по кривой гамма-распределения при Cv = 0 и Cs = 0 и эмпирическая вероятность превышения каждого члена ряда вводится в масштабе клетчатки нормального распределения (табл. 32.1).
Таблица 32.1.
Координаты клетчатки нормального распределения
| Вероятность превышения, % | Расстояния от оси X, мм | Вероятность превышения, % | Расстояния от оси X, мм |
| 0,01 | 75,0 | ||
| 0,02 | 3,3 | 80,5 | |
| 0,05 | 9,5 | 86,0 | |
| 0.1 | 14,0 | 91,8 | |
| 0.2 | 18,7 | 98,6 | |
| 0,33 | 21,8 | 103,0 | |
| 0,5 | 25,1 | 108,1 | |
| 30,5 | 110,7 | ||
| 36,3 | 113,9 | ||
| 39,9 | 116,0 | ||
| 42,8 | 124,7 | ||
| 45,1 | 130,5 | ||
| 52,9 | 99,5 | 135,9 | |
| 62,4 | 99,9 | 147,0 | |
| 69,2 |
Указанная методика, реализованная в виде компьютерной программы «Gist» (Программа «Gist» разработана С.Э. Шпаком), позволяет решать следующие практические задачи:
1. Вычисление коэффициента корреляции для установления наличия (или отсутствия) корреляционной связи Y = f(X):
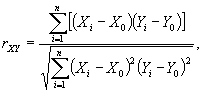 где
где
Хi, Yi - значения координат натурных точек;
X0, Y0 - средние арифметические значения рядов чисел X и Y.
Вычисленное значение коэффициента корреляции rXY сравнивается с минимально допустимым значением rmin = 0,6 и при выполнении условия rXY ³ rmin выполняются дальнейшие расчеты.
2. Ранжирование членов статистического ряда в убывающем порядке и вычисление эмпирической вероятности превышения элементов ряда:
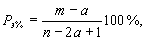 где
где
т - порядковый номер члена ранжированного ряда;
п - общее число членов ряда;
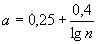 - эмпирический параметр С.М. Бликштейна.
- эмпирический параметр С.М. Бликштейна.
3. Определение коэффициентов аппроксимирующей функции методом «наименьших квадратов»:
У = f(X) = В0 + В1Х + В2Х2 + В3Х3 +...+ ВkХk, где ( 32.1)
В0, В1, ..., Вk - постоянные коэффициенты, подлежащие определению;
k - порядок аппроксимирующей функции (k = 1-5).
Основное положение метода «наименьших квадратов» состоит том, что сумма квадратов отклонений исходных величин от аппроксимирующей функции должна быть минимальной:
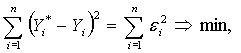 где
где
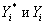 - значение искомой величины, полученное по аппроксимирующей зависимости и фактическое значение исходной величины.
- значение искомой величины, полученное по аппроксимирующей зависимости и фактическое значение исходной величины.
Подставляя в выражение (32.1) все экспериментальные значения исходных точек (Xi, Yi), получим систему из п начальных уравнений:
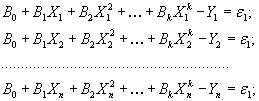 (32.2)
(32.2)
Если уравнение (32.2) записать в развернутом виде, то получим:
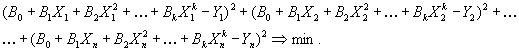 (32.3)
(32.3)
Переменными величинами в этом выражении являются коэффициенты В0, В1, ..., Вk и для них отыскиваются такие значения, при которых выражение (32.3) имеет наименьшую величину. Если для этой цели воспользоваться общим приемом дифференциального исчисления и найти частные производные выражения (32.3) по всем искомым коэффициентам В, приравняв их нулю, окончательно получим:
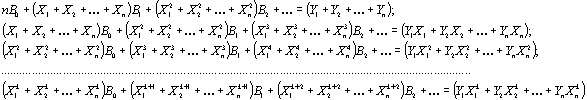 (32.4)
(32.4)
Система (32.4), состоящая из (k+1) линейных уравнений с (k+1) неизвестными коэффициентами В, решается одним из известных способов линейной алгебры (в программе «Gist» реализован «метод исключения Гаусса»). В результате этого решения определяются все (k+1) неизвестных коэффициента В аппроксимирующего уравнения (32.1).
На (рис. 32.1) представлены результаты статистической обработки по программе «Gist» максимальных уровней за 107-летний период наблюдений на р. Иртыш (водомерный пост г. Ханты-Мансийск).
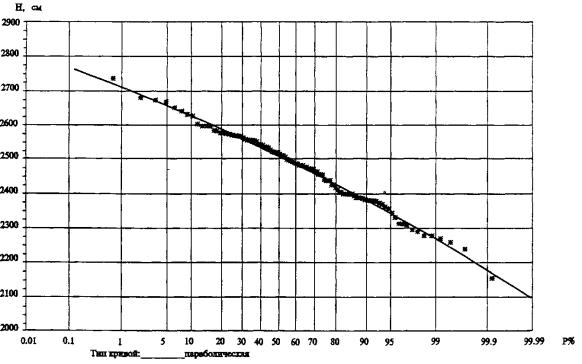
Рис. 32.1. Кривая вероятностей максимальных уровней на р. Иртыш (в/п г. Ханты-Мансийск)
4. Определение среднеквадратического отклонения вычисленных ординат от ординат натурных точек и коэффициента детерминации.
5. Вычисление значений Y при Хmin £ Х £ Хmax с заданным шагом DХ.
6. Вывод на экран монитора или на принтер графика функции Y = f(X) при Хmin £ Х £ Хmax.
7. Вычисление значений X при заданных значениях Y.
8. Вычисление значений Y при заданных значениях X.
9. Вычисление значений гидрометеорологических величин следующих вероятностей превышения Р(%): 0,1; 0,33; 1; 2; 3; 5; 10; 20; 30; 40; 50; 60; 70; 80; 85; 90; 95; 98; 99; 99,5; 99,9.
10. То же для усеченных кривых при (выше средней отметки поймы) Р(%): 0,1; 0,33; 1; 2; 3; 5; 10; 20; 30; 40; 50.
Результаты расчета выводятся на экран монитора, а также в виде таблиц и графиков на принтере (см. рис. 32.1).
Дата добавления: 2017-03-12; просмотров: 2267;











