Уравнение состояния

Повседневный опыт показывает, что в любой предоставленной себе самой, то есть полностью изолированной от внешних воздействий, термодинамической системе со временем происходит выравнивание по объему всех термодинамических параметров. Это – принцип полного термодинамического равновесия (его иногда называют нулевым началом термодинамики). То состояние, к которому самопроизвольно и необратимо (то есть так, что, придя в это состояние, система сама собой не может из него выйти) стремится любая изолированная система, получило название состояния теплового или термодинамического равновесия. Состояние теплового равновесия возможно и в открытых системах при неизменности внешнего воздействия на систему, но об этом подробнее будет сказано в разделе 9.

В состоянии теплового равновесия прекращаются все макроскопические изменения в термодинамической системе, и в таком состоянии система способна оставаться сколь угодно долгое время. Для нарушения теплового равновесия необходимо изменение внешнего воздействия на систему. Самопроизвольные, чаще всего небольшие, отклонения от равновесного состояния термодинамической системы, конечно, случаются (в силу хаотического, взаимно несогласованного характера протекания микропроцессов). Они носят название флуктуаций. Это особый вопрос, рассматриваемый в статистической механике, а в рамках феноменологической равновесной термодинамики флуктуациями просто пренебрегают.

Процесс самопроизвольного перехода системы из неравновесного состояния в состояние равновесное называется процессом релаксации. У разных термодинамических параметров характерное время выравнивания разное. Промежуток времени, характеризующий процесс выравнивания по объему какого-либо из макроскопических параметров, носит название времени релаксации для данного параметра. Время релаксации зависит от микромеханизма процесса релаксации. Для установления состояния полного термодинамического равновесия требуется время, определяемое наибольшим из времен релаксации. За это время устанавливается равновесие по всем параметрам. Следует подчеркнуть, что тепловое равновесие носит динамический характер, то есть сохраняется присутствие микропроцессов, не нарушающих однако состояния теплового равновесия..

В классической термодинамике механизм установления теплового равновесия не играет абсолютно никакой роли, поскольку эта термодинамика имеет дело только с такими термодинамическими системами, где уже установилось тепловое равновесие (или почти установилось, то есть система пренебрежимо мало отклонилась от равновесного состояния). После установления равновесия, на термодинамических параметрах уже никак не отражается наличие или отсутствие между отдельными элементами термодинамического коллектива микровзаимодействий, ответственных за установление в системе теплового равновесия. Именно поэтому можно рассматривать самые простые модели поведения частиц (элементов) системы, где никакой роли не будут играть, например, размеры частиц или законы их взаимодействия, а результаты все равно получаются правильно отражающими наблюдаемые явления (разумеется, в границах применимости используемых моделей). Это замечательное свойство – независимость выводов термодинамики от законов микровзаимодействий, их всеобщность – есть следствие равновесного состояния рассматриваемых термодинамических систем. За это термодинамику иногда называют термостатикой.

Все явления, сопровождающиеся процессами приближения к тепловому равновесию, необратимы. Необратимость процесса в строгом смысле этого слова означает, что процесс нельзя пройти в обратном направлении через те же самые состояния. Так, например, при сжатии газа в колбе под поршнем концентрация молекул газа вблизи поршня больше, чем во всем остальном объеме, а при обратном движении поршня – наоборот, концентрация молекул вблизи поршня меньше. Это означает, что промежуточные состояния термодинамической системы в процессе сжатия и в процессе разрежения газа не идентичны друг другу, и, следовательно, процесс нельзя пройти в обратном направлении в точности через те же самые промежуточные состояния. О термодинамическом понимании необратимости и обратимости мы еще будем говорить, когда вернемся к этому вопросу в третьем разделе.

В механике мы привыкли к тому, что задание начальных значений координат и импульсов частиц однозначно определяет (через решение уравнений движения) их координаты и импульсы (то есть состояние механической системы) в любые другие моменты времени. Это означает, что разные начальные условия ведут к разным конечным состояниям, и, зная уравнение движения, в принципе всегда можно восстановить историю состояний механической системы.

Иное дело термодинамические системы. Каковы бы ни были первоначальные распределения частиц системы по координатам и импульсам, после установления теплового равновесия ничего нельзя сказать об этих начальных условиях. Термодинамическая система «не помнит» историю своих состояний, предшествовавших равновесному состоянию. Ничего нельзя сказать о том, каким путем, через какие промежуточные состояния система шла к равновесию. В равновесной термодинамической системе не сохраняется информация о прошлых ее состояниях. Динамическое описание состояния, используемое в механике, предполагает возможность в любой момент точно указать координаты и импульсы всех частиц системы. В термодинамических системах, состоящих из колоссального числа частиц, движущихся почти независимо друг от друга, возможность такого динамического описания оказывается утраченной. Однако в условиях термодинамического равновесия имеется возможность указать усредненные по времени (или, что то же самое, по коллективу частиц) координаты и импульсы частицы. По сравнению с механикой оказалась утраченной возможность точного знания фазовой траектории отдельной частицы в координатно-импульсном пространстве. Произошла некоторая утрата определенности описания состояния каждой частицы. Мерой утраты этой определенности должна служить новая функция состояния системы, связанная с усредненной величиной разброса («размытостью») значений координат и импульсов частиц около их средних значений. Эта новая функция должна отражать новую (по сравнению с механикой) характеристику системы частиц, которую можно назвать хаотичностью состояния системы. Изменение этой функции при переходе системы из одного состояния в другое означает изменение степени хаотичности состояния системы. Несколько забегая вперед, укажем, что такой функцией является энтропия.

В равновесной термодинамике нет уравнения, аналогичного уравнению движения в механике. Но здесь есть уравнение (равновесного) состояния. Как уже отмечалось, в термодинамике для описания состояния термодинамической системы считается достаточным охарактеризовать ее термодинамическими параметрами, такими как давление, температура и объем, и в ряде случаев еще некоторыми. Обычно этих трех параметров бывает достаточно, если не требуется знания концентраций различных компонентов в смесях (при химических реакциях) и не рассматриваются электрические и магнитные влияния.

Весь накопленный человечеством за его историю опыт, касающийся поведения термодинамических систем, убеждает нас в том, что в состоянии теплового равновесия между термодинамическими параметрами должна существовать связь, позволяющая найти любой из параметров, если известны все остальные. Существование этой связи должно проявляться в виде наличия определенной функциональной зависимости между этими параметрами, называемой уравнением состояния и записываемой в самом общем виде как

f(P,T,V,…) = 0. (1.1)

Существование такого (термического) уравнения состояни означает,что число независимых параметров на единицу меньше, чем их входит в это урапвнение.

Почему мы уверены в существовании такой связи, называемой иногда термическим уравнением состояния?

Дело в том, что из самого факта существования этого уравнения можно извлечь некоторые следствия, которые можно проверить опытным путем. Так, рассматривая в качестве независимых термодинамических параметров тела его давление Р и температуру Т и считая объем функцией этих параметров, мы можем написать для
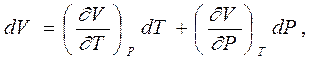дифференциала объема следующее выражение

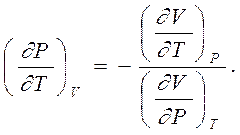которое при неизменном объеме, то есть когда dV = 0, дает связь

Вспомнив используемые в технике три коэффициента, а именно:

-
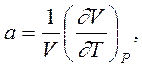изобарный (Р = Const.) коэффициент теплового расширения

- коэффициент изотермической сжимаемости (который обратно пропорционален изотермическому модулю всестороннего сжатия В_Т), где отрицательный знак при нормальной сжимаемости (уменьшение объема при повышении давления) дает положительное значение коэффициента,

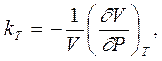и ещё

- изохорный (V = Const.) термический (температурный) коэффициент давления

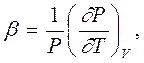то мы получаем (просто из факта существования уравнения состояния, если это предположение справедливо) следующую связь между этими тремя коэффициентами

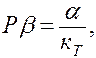позволяющую на практике по любым двум коэффициентам вычислить третий, и проверить правильность этого соотношения экспериментально.

Существование уравнения состояния позволяет в принципе вычислить в равновесном состоянии любой из термодинамических параметров (если известны остальные), и, следовательно, вычислить любые функции состояния термодинамической системы, поскольку (согласно общему принципу макроскопически-описательного изучения термодинамических систем) знания термодинамических параметров (и энергии) вполне достаточно для описания состояния системы, а значит и для вычисления любой из интересующих нас функций состояния этой системы.