Запись ограничений.

Ограничения бывают двух типов. Во-первых, это ограничения на диапазон изменения самих проектных переменных: a_i ≤ x _i≤ b_i, i=1,2,..n. Такие ограничения называются геометрическими. Например, толщина обшивки может быть ограничена конструктивно: δ_min ≤ δ _i≤ δ_max.

Вторым видом ограничений являются функциональные ограничения, связанные с работоспособностью проектируемой системы. На словах они часто выражаются довольно просто, и на первый взгляд кажется, что это просто сделать и математически. Например, «конструкция должна иметь достаточную прочность и долговечность». Это требование включает в себя вычисление напряжений во всех расчётных случаях нагружения (до 36) для каждого элемента конструкции, что предполагает построение адекватной модели конструкции, моделировании нагрузок и проведение вычислений. Всё это требует значительных затрат календарного времени и высокой квалификации инженера-расчётчика.

Ограничения обычно записываются в стандартной форме 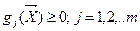. Они выделяют из всего множества проектных переменных подмножество, являющееся областью допустимых проектов. Главная неприятная особенность функциональных ограничений в технических задачах – это то, что они носят алгоритмический характер. Мы не можем по значениям проектных переменных сразу определить, принадлежит ли этот набор параметров области допустимых проектов. Мы должны рассчитать систему с данными значениями проектных переменных, определить её характеристики и сравнить с допустимыми.

Здесь можно провести наглядную аналогию с задачей отыскания наиболее глубокого места озера, но только если дно в этой точке свободно от водорослей. Чтобы замерить глубину и чистоту дна нужно подплыть на лодке в заданную точку, опустить на дно драгу для добывания водорослей и только после того, как драга ничего не принесла, - замерять глубину.

Функциональные и геометрические ограничения могут привести к следующим ситуациям.

1. Допустимая область проектных решений является пустой.

2. Допустимая область проектных решений содержит единственную точку.

3. Допустимая область содержит множество проектных решений.

В первом случае в рамках наложенных ограничений проект реализовать невозможно. Во втором случае проект единственный и ни о какой оптимизации речи не идёт. В третьем случае возможно несколько проектных решений и мы должны выбрать наилучшее, то есть провести оптимизацию.

Построение модели.

Модель является непременным атрибутом оптимизации, поскольку она связывает проектные переменные, характеристики проектируемого объекта и сам объект в процессе функционирования.

Инженерные модели не являются точными копиями реальных объектов, явлений и процессов. Реальность очень сложна и её никогда нельзя смоделировать в полном объёме. Всегда делают допущения и пользуются аппроксимацией. Построение воображаемой модели реального явления – это обычная процедура в инженерной практике. Важно только, чтобы инженер знал о различии между своей моделью и реальным миром. Эти различия определяются допущениями, независимо от того, приняты они сознательно или нет.

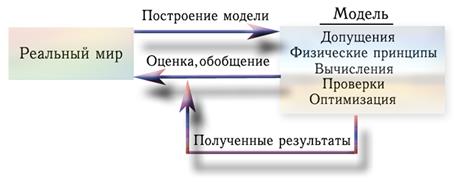
Рис. 4. Построение модели объекта.

К математическим моделям предъявляются следующие требования.

1. Адекватность модели – возможность получения имеющих смысл результатов.

2. Точность модели – согласованность расчётных данных с натурным экспериментом.

3. Быстродействие модели – возможность получения расчётных данных за приемлемое, обычно заданное, календарное время.

4. Работоспособность во всём диапазоне изменения проектных переменных.

Требования (1,2) и 3 противоречивы и поэтому процесс построения модели всегда связан с компромиссом. С одной стороны, адекватность и точность требуют детальных и сложных моделей, учитывающих все переменные, тогда как с другой стороны, время проектирования ограниченно и результат должен быть получен к строго заданному сроку.