Постановка задачи оптимизации.

При решении любой организационной или технической задачи её сначала необходимо сформулировать, то есть ответить на вопросы: 1) С чем мы имеем дело? Каковы функции системы, каковы её связи с внешним окружением? 2) Чего мы хотим? Что нужно сделать, или как нужно сделать? 3) Каковы наши возможности? Какие у нас есть ресурсы для исполнения наших желаний?

Именно здесь совершается много ошибок. Как точно заметил Джон Дьюи: «Хорошо поставленная задача уже наполовину решена». Задача, сведённая к конкретным вопросам, позволяет выразить получаемое решение через величины, которые можно затем вычислить или измерить. Другими словами, нужно ставить такие вопросы, на которые можно получить количественный ответ. Недостаточно ставить вопросы типа: Будет ли самолёт экономичным? Будет ли конструкция работать? Такие вопросы не являются конкретными. Вместо этого нужно ставить вопросы иного характера. Какова будет стоимость тонно-километра при перевозке 30 пассажиров на дальность 1000 км при рейсовой скорости 450 км/час? Какие напряжения возникнут в элементах конструкции при нагрузке 80 кН и нагреве до 300⁰С? Для подготовки таких вопросов, то есть для определения задачи необходимо чёткое понимание реальной физической ситуации и умение рассуждать. Формулировке задачи обычно мешают избыточные условия, которые делают технические задачи неимоверно сложными. И здесь огромную помощь оказывает определение задачи в терминах математического программирования. Согласно ей, при постановке задачи математического программирования необходимо выполнить следующие работы: 1) выбрать функцию цели; 2) выбрать проектные переменные; 3) записать ограничения.

Задача оптимизации формулируется так: найти вектор проектных переменных 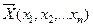, обеспечивающий минимальное значение целевой функции 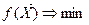при выполнении системы функциональных и геометрических неравенств: .

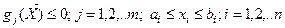Функция цели.

Это критерий качества изделия, процесса или системы, минимума или максимума которого мы хотим достичь. Численное значение функции цели определяет степень совершенства объекта, разработанного в результате проектирования. Функция цели должна быть одна и в этом состоит трудность её выбора.

Нельзя создать самолёт, обладающий максимальной скоростью, высотой и дальностью полёта; нельзя сделать шасси с минимальной массой и максимальной энергоёмкостью; нельзя создать воздушное судно с минимальными затратами на техническое обслуживание и максимальной надёжностью.

Для организационно-технической системы, например при проектировании авиационно-технологической базы, различными руководителями среднего звена могут быть выбраны разные критерии качества системы. В частности:

1. Начальник отдела снабжения отдаст предпочтение проекту, согласно которому производственный процесс протекает с минимальными изменениями в ассортименте расходных материалов и запасных частей. При этом минимизируются затраты по доставке и входному контролю.

2. Руководитель производственного отдела заинтересован в реализации проекта, в соответствии с которым максимальны объемы складских запасов расходных материалов и запасных частей всех видов. В этом случае минимизируется продолжительность интервала времени обслуживания и ремонта воздушных судов между получением заказа от потребителя и его выполнением.

3. Руководитель аэропорта отдаст предпочтение проекту, в соответствии с которым объемы складских запасов минимальны, с тем, чтобы уменьшить капитальные издержки на хранение изделий.

Нетрудно видеть, что эти критерии при оптимизации не могут быть реализованы одновременно.

Здесь мы подошли к вопросу: как быть, если к проекту предъявляются минимаксные требования по многим критериям? Подробные и предельно чёткие ответы на этот вопрос можно найти в книге Д.И.Батищева [2], но из всех рекомендаций по построению единственной функции цели отметим два подхода, чтобы проиллюстрировать общее направление мыслей.

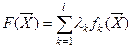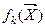1. Метод взвешенных сумм. Функция цели имеет вид: , где - частные критерии качества; λ_k – весовые коэффициенты, показывающие важность отдельного критерия в общей оценке качества проекта.

2. Оценка по потерям. Функция цели имеет вид: 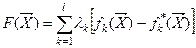. Здесь 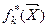- минимальное или максимальное значение частного критерия качества.

Основная трудность в реализации этих подходов состоит в назначении весовых коэффициентов λ_k. От их выбора зависит облик будущего изделия или системы и все их параметры и характеристики. Отметим ещё, что при проектировании одного и того же объекта весовые коэффициенты λ_k в первом и втором подходе могут быть (и зачастую бывают) различными.