Двоичная запись цифровых данных

Алгоритмы и машины Тьюринга

Основы алгоритмов

Как точно определить понятие алго­ритма, или машины Тьюринга, или уни­версальной машины Тьюринга? Почему эти понятия играют одну из главных ролей в со­временном представлении о «мыслящем ус­тройстве»? Есть ли какие-нибудь абсолют­ные ограничения на принципиальные воз­можности использования алгоритмов? Для того чтобы ответить на эти вопросы, нам придется разобраться в деталях, что пред­ставляют собой алгоритм и машины Тью­ринга.

В дальнейших рассуждениях я буду ино­гда прибегать к математическим выражени­ям. Вероятно, некоторых читателей эти вы­кладки напугают и даже заставят отложить книгу в сторону. Если вы как раз такой читатель, то я прошу вашего снисхождения и рекомендую вам последовать совету, дан­ному мной в Обращении к читателю.! Доказательства, которые здесь встретятся, не потребуют владения математическим ап­паратом, выходящим за пределы школьного курса, но чтобы в них детально разобрать­ся, все же понадобятся интеллектуальные усилия. На самом деле, большинство рассу­ждений изложено весьма подробно, и если внимательно им следовать, можно добиться глубокого понимания. Однако, даже беглый просмотр доказательств позволяет ухватить основную идею. С другой стороны, если вы являетесь экспертом в этой области, то я опять вынужден принести свои извине­ния. Но я осмелюсь предположить, что даже в этом случае вам будет небесполезно озна­комиться с моими рассуждениями, в кото­рых почти наверняка найдется что-то инте­ресное и для вас.

Слово «алгоритм» происходит от имени персидского математика IX века Абу Джа-фара Мухаммеда ибн Мусы аль-Хорезми, написавшего около 825 года н. э. руковод­ство по математике Kitab al-jabr wa'l-muqa-bala, которое оказало значительное влия­ние на математическую мысль того времени. Современное написание «алгоритм», при­шедшее на смену более раннему и точно­му «алгоризм», своим происхождением обя­зано, скорее всего, ассоциации со словом «арифметика»). (Примечательно, что и сло­во «алгебра» происходит от арабского al-jabr, фигурирующего в названии вышеупомяну­той книги).

Примеры алгоритмов были, однако, из­вестны задолго до появления книги аль-Хорезми. Один из наиболее известных - алгоритм Евклида — процедура отыскания наибольшего общего делителя двух чисел, восходит к античности (примерно 300 лет до н. э.). Давайте посмотрим, как он рабо­тает. Возьмем для определенности два чи­сла, скажем, 1365 и 3654. Наибольшим об­щим делителем двух чисел называется са­мое большое натуральное число, на которое делится каждое из этих чисел без остат­ка. Алгоритм Евклида состоит в следующем. Мы берем одно из этих чисел, делим его на другое и вычисляем остаток: так как 1365 входит дважды в 3654, в остатке по­лучается 3654 - 2 х 1365 = 924. Далее мы заменяем наши два исходные числа дели­телем (1365) и полученным остатком (924), соответственно, производим с этой парой ту же самую операцию и получаем новый остаток: 1365 - 924 = 441. Для новой пары чисел — а именно, 924 и 441, — получа­ем остаток 42. Эту процедуру надо повто­рять до тех пор, пока очередная пара чисел не поделится нацело. Выпишем эту после­довательность:

3654 : 1365 дает в остатке 924

1365 : 924 дает в остатке 441

924 : 441 дает в остатке 42

441 : 42 дает в остатке 21

42 : 21 дает в остатке 0.

Последнее число, на которое мы делим, а именно 21, и есть искомый наибольший общий делитель.

Алгоритм Евклида является системати­ческой процедурой, которая позволяет найти этот делитель. Мы только что применили эту процедуру к двум конкретным числам, но она работает и в самом общем слу­чае с произвольными числами. Для очень больших чисел эта процедура может за­нять много времени, и будет выполнять­ся тем дольше, чем больше сами числа. Но в каждом конкретном случае выполне­ние процедуры в конце концов заканчи­вается, приводя за конечное число шагов к вполне определенному ответу. На каждом этапе мы точно представляем себе действие, которое должно быть выполнено, и точно знаем, когда получен окончательный ре­зультат. Более того, всю процедуру мож­но описать конечным числом терминов, не­смотря на то, что она может применяться к любым, сколь угодно большим натураль­ным числам. («Натуральными числами» на­зываются неотрицательные 14 целые числа О, 1, 2, 3,4, 5, 6, 7, 8, 9, 10, 11, ... ). На самом деле нетрудно изобразить (конечную) блок-схему, описывающую логическую последо­вательность операций алгоритма Евклида (рис. 2.1).

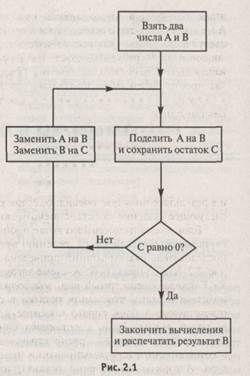
Нужно заметить, что на схеме эта про­цедура не до конца разбита на простей­шие составляющие, поскольку мы неяв­ным образом предположили, что нам уже «известно», как выполнять необходимую ба­зовую операцию получения остатка от деле­ния двух произвольных натуральных чисел А и В. Эта операция, в свою очередь, также алгоритмична и выполняется при помощи хорошо знакомой нам со школы процеду­ры деления. Эта процедура, на самом деле, сложнее, чем все остальные части алгоритма Евклида, но и она может быть представлена в виде блок-схемы. Основное затруднение здесь возникает из-за использования при­вычной «десятичной» записи натуральных чисел, что вынуждает нас выписывать все та­блицы умножения, учитывать перенос и т. п. Если бы для представления некоторого чи­сла п мы использовали последовательность из п каких-нибудь одинаковых знаков, на­пример, пяти звездочек (*****) для обо­значения пятерки, то определение остатка свелось бы к совершенно элементарной ал­горитмической операции. Для того чтобы получить остаток от деления А на В, до­статочно просто убирать из записи числа А последовательность знаков, представля­ющих В, до тех пор, пока на некотором этапе оставшееся число знаков в записи А не станет недостаточным для выполнения следующего шага. Эта последовательность знаков и даст требуемый ответ. Например, желая получить остаток от деления 17 на 5, мы просто будем последовательно удалять ***** из *****************, как это показано ниже:

*****************

************

*******

**

и в результате получим, очевидно, 2, так как следующее удаление уже станет невозможно.

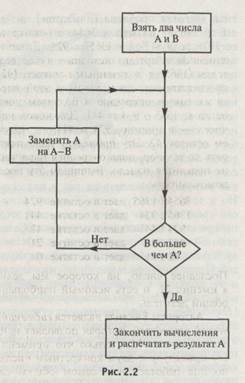
Блок-схема изложенного выше процес­са нахождения остатка от деления путем последовательных вычитаний приведена на рис. 2.2. Чтобы придать блок-схеме алгорит­ма Евклида завершенный вид, мы должны подставить схему отыскания остатка в со­ответствующий блок справа в центре пре­дыдущей схемы. Такая подстановка одно­го алгоритма в другой — распространенная в компьютерном программировании проце­дура. Алгоритм вычисления остатка, изо­браженный на рис. 2.2, служит примером подпрограммы, иначе говоря, это алгоритм (как правило, уже известный), вызываемый и используемый по мере надобности в ходе выполнения основного алгоритма.

Безусловно, обозначение числа n про­сто набором из п звездочек чрезвычайно не­эффективно, когда речь заходит о больших числах. Именно поэтому обычно исполь­зуют более компактную запись, например, стандартную (десятичную) систему. Однако оставим в стороне эффективность операций и обозначений и уделим все внимание во­просу о том, какие операции в принципе мо­гут выполняться алгоритмически. Действие, которое поддается алгоритмизации в одной записи, сохранит это свойство и в любой другой. Эти два случая различаются толь­ко техническими нюансами и сложностью выполнения алгоритма.

Алгоритм Евклида — это лишь одна из многих, часто классических, алгоритми­ческих процедур, встречающихся в матема­тике повсеместно. Но, вероятно, не лиш­ним будет отметить, что, несмотря на значительный исторический возраст отдельных алгоритмов, точная формулировка универ­сального определения алгоритма появилась только в двадцатом веке. В 1930-х годах бы­ло предложено несколько альтернативных формулировок этого понятия, из которых наиболее емкая и убедительная — и, к тому же, наиболее значимая в историческом пла­не — опирается на понятие машины Тьюрин­га. Поэтому нам будет полезно рассмотреть некоторые свойства этих «машин».

Прежде всего следует помнить, что «ма­шина» Тьюринга принадлежит области «аб­страктной математики» и ни в коем слу­чае не является физическим объектом. Это понятие было введено в 1935-1936 годах английским математиком и кибернетиком Аланом Тьюрингом, внесшим огромный но­ваторский вклад в развитие компьютерной науки (Тьюринг [1937]). Тьюринг рассма­тривал задачу весьма общего характера (из­вестную как проблема алгоритмической раз­решимости), которая была поставлена вели­ким немецким математиком Давидом Гиль­бертом частично в 1900 году на Париж­ском Конгрессе математиков (так называемая «десятая проблема Гильберта»), и бо­лее полно — на международном конгрес­се 1928 года в Болонье. Проблема, поста­вленная Гильбертом, состояла ни больше, ни меньше как в отыскании универсаль­ной алгоритмической процедуры для реше­ния математических задач или, вернее, от­вета на вопрос о принципиальной возмож­ности такой процедуры. Кроме того, Гиль­берт сформулировал программу, целью ко­торой было построение математики на не­сокрушимом фундаменте из аксиом и пра­вил вывода, установленных раз и навсегда. Но к тому моменту, когда Тьюринг напи­сал свою великую работу, сама идея этой программы уже была опровергнута порази­тельной теоремой, доказанной в 1931 го­ду блестящим австрийским логиком Кур­том Геделем. Мы рассмотрим теорему Геделя и ее значение в четвертой главе. Пробле­ма Гильберта, которую исследовал Тьюринг (Entscheidungsproblem), не зависит от какого-либо конкретного построения математики в терминах аксиоматической системы. Во­прос формулировался так: существует ли не­кая универсальная механическая процедура, позволяющая, в принципе, решить все ма­тематические задачи (из некоторого вполне определенного класса) одну за другой?

Трудность с ответом на этот вопрос бы­ла связана отчасти с определением смысла «механической процедуры» — это понятие выходило за рамки стандартных математи­ческих идей того времени. Чтобы как-то ее преодолеть, Тьюринг постарался предста­вить, как можно было бы формализовать по­нятие «машина» путем расчленения ее дей­ствий на элементарные операции. Вполне вероятно, что в качестве примера «маши­ны», помимо прочего, Тьюринг рассматри­вал и человеческий мозг, тем самым относя к «механическим процедурам» все действия, которые математики выполняют, размыш­ляя над решением математических задач.

Хотя такой взгляд на процесс мыш­ления оказался весьма полезным при раз­работке Тьюрингом его в высшей степени важной теории, нам совершенно необяза­тельно его придерживаться. Действительно, дав точное определение механической про­цедуры, Тьюринг тем самым показал, что су­ществуют совершенно четко определенные математические операции, которые никак не могут называться механическими в обще­принятом смысле слова. Можно, наверное, усмотреть некую иронию в том, что эта сто­рона работы Тьюринга позволяет нам теперь косвенным образом выявить его собствен­ную точку зрения на природу мышления. Однако, нас это пока занимать не будет. Прежде всего нам необходимо выяснить, в чем же, собственно, заключается теория Тьюринга.

Концепция Тьюринга

Попробуем представить себе устрой­ство, предназначенное для выполнения не­которой (конечноопределенной) вычисли­тельной процедуры. Каким могло бы быть такое устройство в общем случае? Мы долж­ны быть готовы к некоторой идеализации и не должны обращать внимания на практи­ческие аспекты — мы на самом деле рассма­триваем математическую идеализацию «ма­шины». Нам нужно устройство, способное принимать дискретное множество различ­ных возможных состояний, число которых конечно (хотя и может быть очень боль­шим). Мы назовем их внутренними состо­яниями устройства. Однако мы не хотим, чтобы объем выполняемых на этом устрой­стве вычислений был принципиально огра­ничен. Вспомним описанный выше алго­ритм Евклида. В принципе, не существует предельной величины числа, после которой алгоритм перестает работать. Этот алгоритм, или некая общая вычислительная процедура, будет тем же самым независимо от того, сколь велики числа, к которым он применя­ется. Естественно, для очень больших чисел выполнение процедуры может занять много времени и может потребоваться огромное количество «черновиков» для выполнения пошаговых вычислений. Но сам по себе ал­горитм останется тем же конечным набором инструкций, сколь бы большими ни были эти числа.

Значит, несмотря на конечность чи­сла внутренних состояний, наше устрой­ство должно быть приспособлено для работы с входными данными неограниченного объ­ема. Более того, устройство должно иметь возможность использовать внешнюю память неограниченного объема (наши «чернови­ки») для хранения данных, необходимых для вычислений, а также уметь выдавать оконча­тельное решение любого размера. Посколь­ку наше устройство имеет только конечное число различных внутренних состояний, мы не можем ожидать, что оно будет «хранить внутри себя» все внешние данные, равно как и результаты своих промежуточных вычи­слений. Напротив, оно должно обращаться только к тем данным и полученным ре­зультатам, с которыми оно работает непо­средственно в настоящий момент, и уметь производить над ними требуемые (опять же, в данный момент) операции. Далее, устройство записывает результаты этих опе­раций — возможно, в отведенной для этого внешней памяти — и переходит к следующе­му шагу. Именно неограниченные объемы входных данных, вычислений и окончатель­ного результата говорят о том, что мы имеем дело с идеализированным математическим объектом, который не может быть реали­зован на практике (рис. 2.3). Но подобная идеализация является очень важной. Чудеса современных компьютерных технологий по­зволяют создавать электронные устройства хранения информации, которые мы можем рассматривать как неограниченные в прило­жении к большинству практических задач.

На самом деле память устройства, кото­рая выше была названа «внешней», можно рассматривать как внутренний компонент современного компьютера. Но это уже тех­нические детали — рассматривать часть объ­ема для хранения информации как внутрен­нюю или внешнюю по отношению к устройству. Одним из способов проводить такое де­ление между «устройством» и «внешней» ча­стью могло бы стать использование понятий аппаратного (hardware) и программного (soft­ware) обеспечения вычислений. В этой тер­минологии внутренняя часть могла бы соот­ветствовать аппаратному обеспечению (hard­ware), тогда как внешняя — программному обеспечению (software). Я не буду жестко при­держиваться именно этой классификации, однако, какую бы точку зрения мы не заня­ли, не вызывает сомнений, что идеализация Тьюринга достаточно точно аппроксимиру­ется современными электронными компью­терами.

Тьюринг представлял внешние данные и объем для хранения информации в ви­де «ленты» с нанесенными на нее метками. Устройство по мере необходимости могло обращаться к этой ленте, «считывать» с нее информацию и перемещать ее вперед или назад в ходе выполнения операций. Поми­мо этого, устройство могло ставить новые метки на ленту и стирать с нее старые, что позволяло использовать одну и ту же ленту и как внешнюю память (то есть «чер­новик»), и как источник входных данных. На самом деле, не стоило бы проводить явное различие между этими двумя поняти­ями, поскольку во многих операциях про­межуточные результаты вычислений могут играть роль новых исходных данных. Вспо­мним, что при использовании алгоритма Евклида мы раз за разом замещали исход­ные числа (А и В) результатами, получен­ными на разных этапах вычислений. Сход­ным образом та же самая лента может быть использована и для вывода окончательного результата («ответа»). Лента будет двигать­ся через устройство туда-сюда до тех пор, пока выполняются вычисления. Когда, на­конец, все вычисления закончены, устрой­ство останавливается, и результат вычисле­ний отображается на части ленты, лежащей по одну сторону от устройства. Для опре­деленности будем считать, что ответ всегда записывается на части ленты, расположен­ной слева от устройства, а все исходные чи­словые данные и условия задачи — на части ленты, расположенной справа от него.

Меня всегда несколько смущало пред­ставление о конечном устройстве, которое двигает потенциально бесконечную ленту вперед и назад. Неважно, насколько ле­гок материал ленты — сдвинуть бесконечную ленту все-таки будет трудно! Вместо этого я предпочитаю представлять себе эту ленту как некое окружение, по которому может перемещаться наше конечное устройство. (Конечно же, в современных электронных устройствах ни «лента», ни само «устрой­ство» не должны в обычном смысле фи­зически «перемещаться», но представление о таком «движении» позволяет достичь из­вестной наглядности.) При таком подходе устройство получает все входные данные из этого окружения, использует его в ка­честве «черновика» и, наконец, записывает в него конечный результат.

В представлении Тьюринга «лента» со­стоит из бесконечной в обоих направлени­ях линейной последовательности квадратов. Каждый квадрат либо пуст, либо помечен. Использование помеченных и пустых ква­дратов означает, что мы допускаем разбие­ние нашего «окружения» (т. е. ленты) на ча­сти и возможность его описания множе­ством дискретных элементов (в противо­положность непрерывному описанию). Это представляется вполне разумным, если мы хотим, чтобы наше устройство работало на­дежно и совершенно определенным обра­зом. В силу используемой математической идеализации мы допускаем (потенциаль­ную) бесконечность «окружения», однако в каждом конкретном случае входные дан­ные, промежуточные вычисления и оконча­тельный результат всегда должны быть ко­нечными. Таким образом, хотя лента и имеет бесконечную длину, на ней должно быть конечное число непустых квадратов. Дру­гими словами, и с той, и с другой сто­роны от устройства найдутся квадратики, после которых лента будет абсолютно пу­стой. Мы обозначим пустые квадраты сим­волом «0», а помеченные — символом «1», например:

Нам нужно, чтобы устройство «считы­вало» информацию с ленты. Мы будем счи­тать, что оно считывает по одному квадра­ту за раз и смещается после этого ровно на один квадрат влево или вправо. При этом мы не утрачиваем общности рассуждений: устройство, которое читает за один раз п квадратов или перемещается на k квадратов, легко моделируется устройством, указанным выше. Передвижение на k квадратов мож­но построить из k перемещений по одному квадрату, а считывание п квадратов за один прием сводится к запоминанию результа­тов п однократных считываний.

Что именно может делать такое устрой­ство? Каким образом в самом общем случае могло бы функционировать устройство, на­званное нами «механическим»? Вспомним, что число внутренних состояний нашего ус­тройства должно быть конечным. Все, что нам надо иметь в виду помимо этого — это то, что поведение нашего устройства пол­ностью определяется его внутренним со­стоянием и входными данными. Входные данные мы упростили до двух символов «0» и «1». При заданном начальном состо­янии и таких входных данных устройство должно работать совершенно определенным образом: оно переходит в новое состояние (или остается в прежнем), заменяет считан­ный символ 0 или 1 тем же или другим символом 1 или 0, передвигается на один квадрат вправо или влево, и наконец, оно решает, продолжить вычисления или же за­кончить их и остановиться.

Чтобы явно определить операции, про­изводимые нашим устройством, для нача­ла пронумеруем его внутренние состояния, например: 0, 1, 2, 3, 4, 5. Тогда действия на­шего устройства, или машины Тьюринга, полностью определялись бы неким явным списком замен, например:

Выделенная цифра слева от стрелки - это символ на ленте, который устройство в данный момент считывает. Оно заменяет этот символ выделенной цифрой в середине справа от стрелки. R означает, что устрой­ство должно переместиться вдоль ленты на один квадрат вправо, a L соответствует тако­му же перемещению влево. (Если, в соответ­ствии с исходным представлением Тьюрин­га, мы полагаем, что движется не устрой­ство, а лента, то R означает перемещение ленты на один квадрат влево, a L — вправо.) Слово STOP означает, что вычисления за­вершены и устройство должно остановиться. Например, вторая инструкция 01 —> 131L говорит о том, что если устройство нахо­дится в начальном состоянии 0 и считывает с ленты 1, то оно должно перейти в состо­яние 13, оставить на ленте тот же символ 1 и переместиться по ленте на один квадрат влево. Последняя же инструкция 2591 —> OOR.STOP говорит о том, что если устройство находится в состоянии 259 и считы­вает с ленты 1, то оно должно вернуться в состояние 0, стереть с ленты 1, т. е. за­писать в текущий квадрат 0, переместиться по ленте на один квадрат вправо и прекра­тить вычисления.

Вместо номеров 0, 1, 2, 3, 4, 5,... для обозначения внутренних состояний мы мо­жем — и это более соответствовало бы зна­ковой системе нанесения меток на ленту — прибегнуть к системе нумерации, построен­ной только на символах «0» и «1». Состо­яние п можно было бы обозначить просто последовательностью из п единиц, но та­кая запись неэффективна. Вместо этого мы используем двоичную систему счисления, ставшую теперь общепринятой:

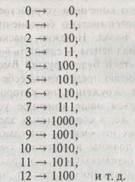
Здесь последняя цифра справа соот­ветствует «единицам» точно так же, как и в стандартной (десятичной) системе запи­си, но цифра прямо перед ней показывает число «двоек», а не «десятков». В свою оче­редь третья цифра справа относится не к «сотням», а к «четверкам»; четвертая -к «восьмеркам», а не к «тысячам» и т. д. При этом разрядность каждой последую­щей цифры (по мере продвижения влево) дается соответственной степенью двойки: 1, 2, 4 (= 2 х 2), 8 (= 2 х 2 х 2), 16 (= 2 x 2 x 2 x 2), 32 (= 2 x 2 x 2 x 2 x 2). (В даль­нейшем нам будет иногда удобно использо­вать в качестве основания системы счисле­ния числа, отличные от «2» и «10». Напри­мер, запись десятичного числа 64 по осно­ванию «три» даст 2101, где каждая ци­фра теперь — некоторая степень тройки: 64 = ( 2 х З³ ) + З² + 1.

Используя двоичную запись для вну­тренних состояний, можно представить вы­шеприведенную инструкцию, описывающую машину Тьюринга, следующим обра­зом:

Здесь я к тому же сократил R.STOP до STOP, поскольку мы вправе считать, что L.STOP никогда не происходит, так как ре­зультат последнего шага вычислений, бу­дучи частью окончательного ответа, всегда отображается слева от устройства.

Предположим, что наше устройство на­ходится во внутреннем состоянии, пред­ставленном бинарной последовательностью 11010010, и процессу вычисления соответ­ствует участок ленты, изображенный на с. 46. Пусть мы задаем команду:

Та цифра на ленте, которая в данный момент считывается (в нашем случае цифра «0»), показана «жирным» символом справа от по­следовательности нулей и единиц, обозна­чающих внутреннее состояние.

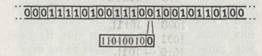
В частично описанном выше приме­ре машины Тьюринга (который я выбрал более-менее произвольно) считанный «0» был бы тогда замещен на «1», внутреннее состояние поменялось бы на «11» и устрой­ство переместилось бы на один шаг влево:

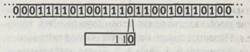
Теперь устройство готово к считыва­нию следующей цифры, снова «О». Соглас­но таблице, оно оставляет этот «0» нетрону­тым, но изменяет свое внутреннее состояние на «100101» и передвигается по ленте назад, т. е. на один шаг вправо. Теперь оно счи­тывает «1» и находит где-то ниже в табли­це инструкцию, которая определяет изме­нение внутреннего состояния и указывает, должна ли быть изменена считанная цифра и в каком направлении по ленте должно дальше двигаться устройство. Таким обра­зом устройство будет действовать до тех пор, пока не достигнет команды STOP. В этой точке — после еще одного шага вправо -раздастся звонок, оповещающий оператора о том, что вычисления завершены.

Мы будем считать, что машина всегда начинает с внутреннего состояния «0» и что вся лента справа от устройства изначально пуста. Все ттструкции и данные подаются в устройство с правой стороны. Как упоми­налось ранее, эта информация всегда имеет форму конечной строки из нулей и единиц, за которой следует пустая лента (т. е. нули). Когда машина получает команду STOP, ре­зультаты вычислений оказываются на ленте слева от считывающего устройства.

Поскольку мы хотели бы иметь возмож­ность вводить в устройство и числовые дан­ные, то нам потребуется некий способ опи­сания обычных чисел (под которыми я здесь имею в виду целые неотрицательные числа 0, 1, 2, 3, 4,...) как части входной инфор­мации. Для представления числа п можно было бы просто использовать строку из п единиц (хотя при этом могут возникнуть трудности, когда речь зайдет о нуле):

Эта примитивная схема нумерации на­зывается (хотя и довольно нелогично) унар­ной (единичной) системой. В этом случае символ 0 мог бы использоваться в каче­стве пробела для разделения двух разных чи­сел. Наличие такого способа разделения для нас существенно, так как многие алгоритмы оперируют не отдельными числами, а мно­жествами чисел. Например, для выполне­ния алгоритма Евклида наше устройство должно производить определенные действия над парой чисел А и В. Соответствующая ма­шина Тьюринга может быть легко записа­на в явном виде. В качестве упражнения заинтересованный читатель может прове­рить, что нижеследующий набор инструк­ций действительно описывает машину Тью­ринга (которую я буду называть EUC), вы­полняющую алгоритм Евклида, если в ка­честве исходных данных использовать два «унарных» числа, разделенных символом 0:

Однако я бы порекомендовал такому читателю начать не с этого упражнения, а с чего-нибудь гораздо более простого, на­пример, с машины Тьюринга UN + 1, ко­торая просто прибавляет единицу к числу в унарном представлении:

Чтобы убедиться в том, что UN+1 на самом деле производит такую операцию, давайте мысленно применим ее, скажем, к ленте вида

соответствующей числу четыре. Мы будем полагать, что наше устройство сначала на­ходится где-то слева от последовательности единиц. Находясь в исходном состоянии О, оно считывает 0, в соответствии с первой инструкцией сохраняет его неизмененным, после чего перемещается на шаг вправо, оставаясь во внутреннем состоянии 0. Оно продолжает последовательно передвигаться вправо до тех пор, пока не встретит первую единицу. После этого вступает в силу вторая инструкция: устройство оставляет единицу как есть и сдвигается на шаг вправо, но уже в состоянии 1. В соответствии с четвертой инструкцией оно сохраняет внутреннее со­стояние 1, равно как и все считываемые еди­ницы, двигаясь вправо до встречи с первым после набора единиц нулем. Тогда начина­ет действовать третья инструкция, соглас­но которой устройство заменяет этот нуль на 1, перемещается на один шаг вправо (вспомним, что команда STOP эквивалент­на R.STOP) и останавливается. Тем самым к последовательности из четырех единиц прибавляется еще одна, превращая — как и требовалось — 4 в 5.

В качестве несколько более трудного упражнения можно проверить, что машина UN x 2, определяемая набором инструкций

удваивает унарное число, как и должно быть, судя по ее названию.

Чтобы понять, как работает машина EUC,нужно явным образом задать пару под­ходящих чисел, скажем, 6 и 8. Как и ранее, изначально машина находится во внутрен­нем состоянии 0 и расположена слева, а лен­та выглядит следующим образом:

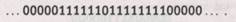
После того, как машина Тьюринга после большого числа шагов останавливается, мы получаем ленту с записью вида

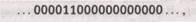
при этом машина располагается справа от ненулевых цифр. Таким образом, найден­ный наибольший общий делитель равен 2 (как и должно быть).

Исчерпывающее объяснение, почему ма­шина EUC (или UN x 2) на самом деле осуществляет действие, для которого она предназначена, включает в себя некоторые тонкости, и разобраться в нем, может быть, даже труднее, чем понять устройство са­мой машины — довольно обычная ситуа­ция с компьютерными программами! (Что­бы полностью понять, почему алгоритми­ческие процедуры делают то, что от них ожидается, необходима определенная инту­иция. А не являются ли интуитивные про­зрения сами алгоритмическими? Это один из вопросов, которые будут для нас важны в дальнейшем.) Я не буду пытаться дать здесь такое объяснение для приведенных приме­ров EUC или UN x 2. Читатель, шаг за ша­гом проверив их действие, обнаружит, что я незначительно изменил обычный алгоритм Евклида, чтобы получить более компакт­ную запись в рамках используемой схемы. И все же описание EUC остается достаточно сложным, включая в себя 22 элементарные инструкции для 11 различных внутренних состояний. В основном эти сложности носят чисто организационный характер. Можно отметить, например, что из этих 22 инструк­ций только 3 в действительности изменяют запись на ленте! (Даже для UN x 2 я исполь­зовал 12 инструкций, половина из которых меняют запись на ленте.)

Двоичная запись цифровых данных

Унарная система чрезвычайно неэф­фективна для записи больших чисел. Поэто­му мы по большей части будем использовать вышеописанную двоичную систему. Однако, сделать это напрямую и попытаться читать ленту просто как двоичное число мы не смо­жем. Дело в том, что мы не имеем возможно­сти сказать, когда кончается двоичное пред­ставление числа и начинается бесконечная последовательность нулей справа, которая отвечает пустой ленте. Нам нужен способ как-то обозначать конец двоичной записи числа. Более того, часто нам будет нуж­но вводить в машину несколько чисел, как, например, в случае с алгоритмом Евклида, когда требуется пара чисел '²'. Но в двоич­ном представлении мы не можем отличить пробелы между числами от нулей или стро­чек нулей, входящих в записи этих двоич­ных чисел. К тому же, помимо чисел нам может понадобиться и запись всевозмож­ных сложных инструкций на той же ленте. Для того чтобы преодолеть эти трудности, воспользуемся процедурой, которую я буду в дальнейшем называть сокращением и со­гласно которой любая строчка нулей и еди­ниц (с конечным числом единиц) не просто считывается как двоичное число, но заме­щается строкой из нулей, единиц, двоек, троек и т.д. таким образом, чтобы каждое число в получившейся строчке соответство­вало числу единиц между соседними нулями в исходной записи двоичного числа. Напри­мер, последовательность:

превратиться в

Мы теперь можем считывать числа 2, 3, 4, ... как метки или инструкции опреде­ленного рода. Действительно, пусть 2 будет просто «запятой», указывающей на пробел между двумя числами, а числа 3, 4, 5, ... могли бы по нашему желанию символизиро­вать различные инструкции или необходи­мые обозначения, как, например, «минус», «плюс», «умножить», «перейти в позицию со следующим числом», «повторить пре­дыдущую операцию следующее число раз» и т.п. Теперь у нас есть разнообразные по­следовательности нулей и единиц, разде­ленные цифрами большей величины. Эти последовательности нулей и единиц будут представлять собой обычные числа, запи­санные в двоичной форме. Тогда записанная выше строка (при замене двоек «запятыми») примет вид:

Используя обычные арабские числа «9», «3», «4», «О» для записи соответствующих двоич­ных чисел 1001, 11, 100и 0,получаем но­вую запись всей последовательности в виде:

Такая процедура дает нам, в частно­сти, возможность указывать, где заканчива­ется запись числа (и тем самым отделять ее от бесконечной полосы пустой ленты спра­ва), просто используя запятую в конце этой записи. Более того, она позволяет закоди­ровать любую последовательность натураль­ных чисел, записанных в двоичной систе­ме, как простую последовательность нулей и единиц, в которой для разделения чисел мы используем запятые. Посмотрим, как это сделать, на конкретном примере. Возьмем последовательность:

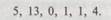
В двоичном представлении она эквивалент­на последовательности

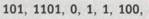
что на ленте можно записать с помощью операции расширения (обратной по отноше­нию к описанной выше процедуре сокраще­ния) как

Такое кодирование легко выполнить, если в исходной двоичной записи чисел про­вести следующие замены:

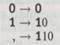
и после этого добавить бесконечные после­довательности нулей с обеих сторон вновь полученной записи. Чтобы сделать более по­нятной эту процедуру в применении к наше­му примеру, разделим полученные двоичные числа пробелами:

Я буду называть этот способ представле­ния (наборов) чисел расширенной двоичной записью. (Так, в частности, в расширенной двоичной форме записи число 13 выглядит как 1010010.)

Есть еще одно, последнее, замечание, которое надо сделать в связи с этой систе­мой записи. Это не более, чем техничес­кая деталь, но она необходима для полно­ты изложения. Двоичная (или десятич­ная) запись натуральных чисел в некоторой степени избыточна в том смысле, что ну­ли, расположенные слева от записи числа, «не считаются» и обычно опускаются, так что 00110010представляет собой то же са­мое двоичное число, что и 110010(а 0050 — то же самое десятичное число, что и 50). Эта избыточность распространяется и на нуль, который может быть записан и как 000, и как 00, и, конечно, как 0. На самом деле и пустое поле, если рассуждать логически, должно обозначать нуль! В обычном пред­ставлении это привело бы к большой пута­нице, но в описанной выше системе коди­рования никаких затруднений не возникает: нуль между двумя запятыми можно запи­сать просто в виде двух запятых, следующих подряд (,,). На ленте такой записи будет со­ответствовать код, состоящий из двух пар единиц, разделенных одним нулем:

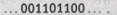
Тогда исходный набор из шести чисел может быть записан в двоичной форме как

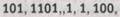
и на ленте при кодировании в расширен­ной двоичной форме мы получим последо­вательность

в которой на один нуль меньше по сравне­нию с предыдущим кодом того же набора.

Теперь мы можем рассмотреть машину Тьюринга, реализующую, скажем, алгоритм Евклида в применении к паре чисел, за­писанных в расширенной бинарной форме. Для примера возьмем ту же пару чисел — 6 и 8, которую мы брали ранее. Вместо преж­ней унарной записи

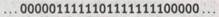
воспользуемся двоичным представлением 6 и 8, т.е. ПО и 1000, соответственно. Тогда эта пара имеет вид: 6, 8, или в двоичной форме 110, 1000, и в расширенной двоичной записи на ленте она будет выглядеть следующим образом

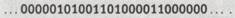
Для этой конкретной пары чисел двоичная форма записи не дает никакого выигрыша по сравнению с унарной. Предположим, од­нако, что мы берем для вычислений (деся­тичные) числа 1 583 169 и 8610. В двоичной записи они имеют вид

На ленте при расширенном двоичном коди­ровании им будет соответствовать последо­вательность

которая занимает менее двух строк, тогда как для у