Виды движения. Действующие силы

Движение реальных жидкостей может быть ламинарным (слоистым) или турбулентным (беспорядочным). Ламинарным движение бывает в тех случаях, когда силы трения, обусловленные вязкостью жидкости, велики по сравнению с силами инерции. К таким случаям относятся просачивание воды через поры грунта и течение очень вязких жидкостей (смолы, смазочного масла, вазелина). Если силы вязкости относительно малы, движение становится турбулентным. Отношение сил инерции к силам вязкости принято характеризовать безразмерной величиной, известной под названием числа Рейнольдса. В общем случае оно имеет вид

.

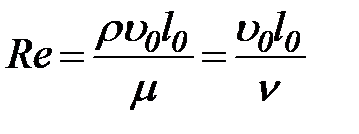где: u₀ – характерная скорость;

l₀ – характерный поперечный размер потока;

r – плотность жидкости;

m – абсолютный коэффициент вязкости;

n = m/r – кинематический коэффициент вязкости.

Значения коэффициента n для воды имеют порядок 1·10^-6м²/с.

Применительно к речным потокам

.

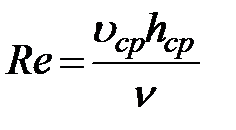где: u_ср – средняя скорость потока;

h_ср – средняя глубина потока.

Ламинарное движение в открытых руслах наблюдается при значениях числа Рейнольдса, меньших его критического значения .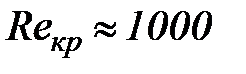
У всех естественных потоков значения чисел Рейнольдса гораздо выше – обычно они составляют 10⁵-10⁷. В соответствии с этим движение воды в реках всегда турбулентное.

Внешнее проявление турбулентности состоит в том, что частицы воды, движущиеся вдоль русла, испытывают случайные отклонения от общего направления движения и случайные колебания продольной скорости. Вследствие этого траектории частиц имеют извилистый вид. В фиксированной точке пространства М(х, у, z) турбулентность вызывает пульсацию скоростей, т.е. случайные колебания всех трех компонент скорости во времени. Чтобы получить упорядоченную картину движения, эти колеблющиеся скорости следует осреднить. Операция временного осреднения компоненты скорости по какому-нибудь координатному направлению, например х, выражается формулой

,

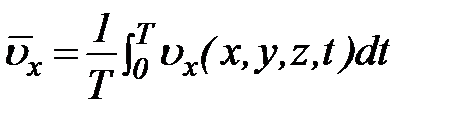где осредненная скорость в точке М (х, у, z) отмечена чертой сверху, а Т есть период осреднения.

Чтобы иметь устойчивое значение осредненной скорости в точке речного потока, достаточно произвести осреднение за период Т, равный 2-3 мин. Выполнив операцию осреднения, можно представить значение компоненты скорости в данной точке в произвольный момент времени t в виде суммы осредненной и пульсационной скоростей:

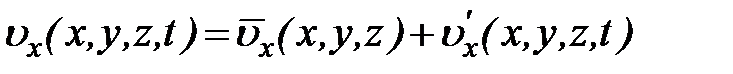. (39)

Пульсационная скорость 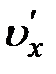является, очевидно, знакопеременной величиной: 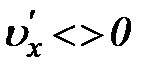. Компонента осредненной скорости по одному или двум координатным направлениям может оказаться нулем, но средние квадратичные значения пульсационных скоростей 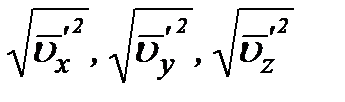все отличны от нуля. Пульсационное движение всегда трехмерное. В толще потока средние квадратичные пульсационные скорости выражаются сотыми и десятыми долями осредненных скоростей.

Случайные отклонения жидких частиц от общего направления движения приводят к перемешиванию жидкости. Турбулентное перемешивание воды в реках оказывает сильнейшее влияние на все идущие в них
гидро- и термодинамические процессы. Особенно велико значение перемешивания воды по вертикали, в ходе которого слои потока, прилегающие ко дну, обмениваются с верхними слоями количеством движения, теплом, растворенными веществами, взвешенными твердыми частицами. Результатом перемешивания является выравнивание распределений скоростей, тепла и других, субстанций, содержащихся в жидкости. Эти распределения в турбулентном потоке значительно равномернее, чем в ламинарном.

В настоящем кратком курсе будем пользоваться феноменологическими способами учета турбулентного перемешивания, не требующими количественной оценки пульсационных скоростей. Таким образом, дальше будем иметь дело только с осредненными скоростями и поэтому для простоты записей знак осреднения над буквой u будем опускать.

Во многих случаях есть возможность применять и еще более простые кинематические модели движения, в которых осреднение скоростей во времени дополнено их осреднением по некоторым областям пространства. Результатами такого комбинированного временного и пространственного осреднения являются: средние скорости на вертикалях

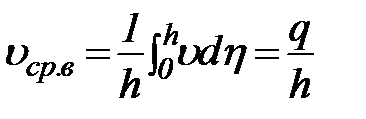(40)

и средние скорости в живых сечениях

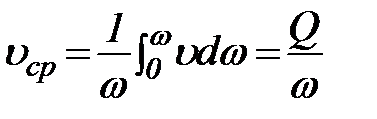. (41)

В этих формулах h – расстояние точки вертикали от дна, а u – проекция вектора местной осредненной скорости на нормаль к поверхности живого сечения. Величина q называется элементарным или удельным расходом воды. В большинстве случаев поверхности живых сечений считаются плоскими.

Мысленно отбросив турбулентные пульсации, будем называть движение установившимся, если элементы осредненного движения (осредненные скорости, осредненное давление и т.д.) не изменяются с течением времени. Если движение изменяется во времени, его называют неустановившимся. Вследствие колебаний стока осредненное движение воды в реках неустановившееся, однако в межень всегда можно выделить отрезки времени – несколько суток (иногда одну – две недели), в течение которых движение допустимо считать установившимся.

Формула (39) мгновенной скорости турбулентного течения относится к установившемуся движению. Если движение неустановившееся, меняется во времени не только пульсационная скорость, но и осредненная, хотя гораздо медленнее, чем первая.

В зависимости от распределения скоростей вдоль потока различают движение равномерное и неравномерное. Движение называется равномерным, если скорости течения вдоль потока не изменяются ни по абсолютной величине, ни по направлению. Если скорости изменяются вдоль потока, движение называется неравномерным. Вследствие сложных геометрических форм речных русел и их кривизны осредненное движение воды в реках, как правило, неравномерное. Однако имеется важное исключение из этого правила – движение воды в прямолинейных плесовых лощинах, где оно очень близко к равномерному.

Вода движется в реках под действием трех сил: силы тяжести, силы трения и Кориолисовой силы инерции. Последняя сила мала по сравнению с двумя другими и в практических задачах ее влиянием пренебрегают.

В речной гидравлике часто находит применение принцип Даламбера, т.е. сведение задачи динамики к задаче статики посредством введения фиктивных сил инерции. Последние для частицы жидкости определяются как произведение массы частицы на ее ускорение, взятое с обратным знаком. Типичным и очень важным применением принципа Даламбера служит включение в число сил, действующих на частицы воды, движущиеся по изогнутому участку русла, центробежной силы инерции (см. п.3.5).

Во избежание недоразумения заметим, что мы считаем Кориолисову силу инерции реальной силой потому, что все системы отсчета, связанные с вращающейся Землей, не являются инерциальными. Когда мы говорим о центробежной силе, действующей в речном потоке, мы отвлекаемся от вращения Земли и считаем, что, стоя на берегу реки, находимся в покое. Тем самым мы вводим местную инерциальную систему отсчета, по отношению к которой центробежная сила в движущейся воде является фиктивной. Если перейти к системе отсчета, связанной с плывущим по реке плотом (не инерциальной), центробежная сила превратится в реальную.

Картина здесь точно такая же, как при движении средств транспорта. При повороте трамвая его пассажир воспринимает центробежную силу как реальную – она заставляет его пошатнуться, т.е. испытать ускорение. С точки зрения человека, стоящего на тротуаре, центробежная сила фиктивна. В его представлении тело пассажира просто стремится сохранить состояние прямолинейного движения.

2.2. Уравнение равномерного движения.
Определение сил трения

В равномерных потоках, например при движении воды в прямолинейной плесовой лощине, сила тяжести уравновешена силой гидравлического трения. В открытых руслах равенство этих сил выражается уравнением (42). Касательное напряжение на дне

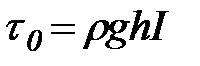. (42)

где: r – плотность воды;

g – ускорение свободного падения;

h – глубина;

I – уклон.

Произведение rh есть масса столба воды, высотой h и с площадью основания, равной единице; произведение gI есть составляющая ускорения свободного падения, направленная по течению, т.е. параллельно свободной поверхности и дну (рис. 21). Таким образом, правая часть уравнения (42) выражает проекцию веса выделенного столба жидкости на направление движения.

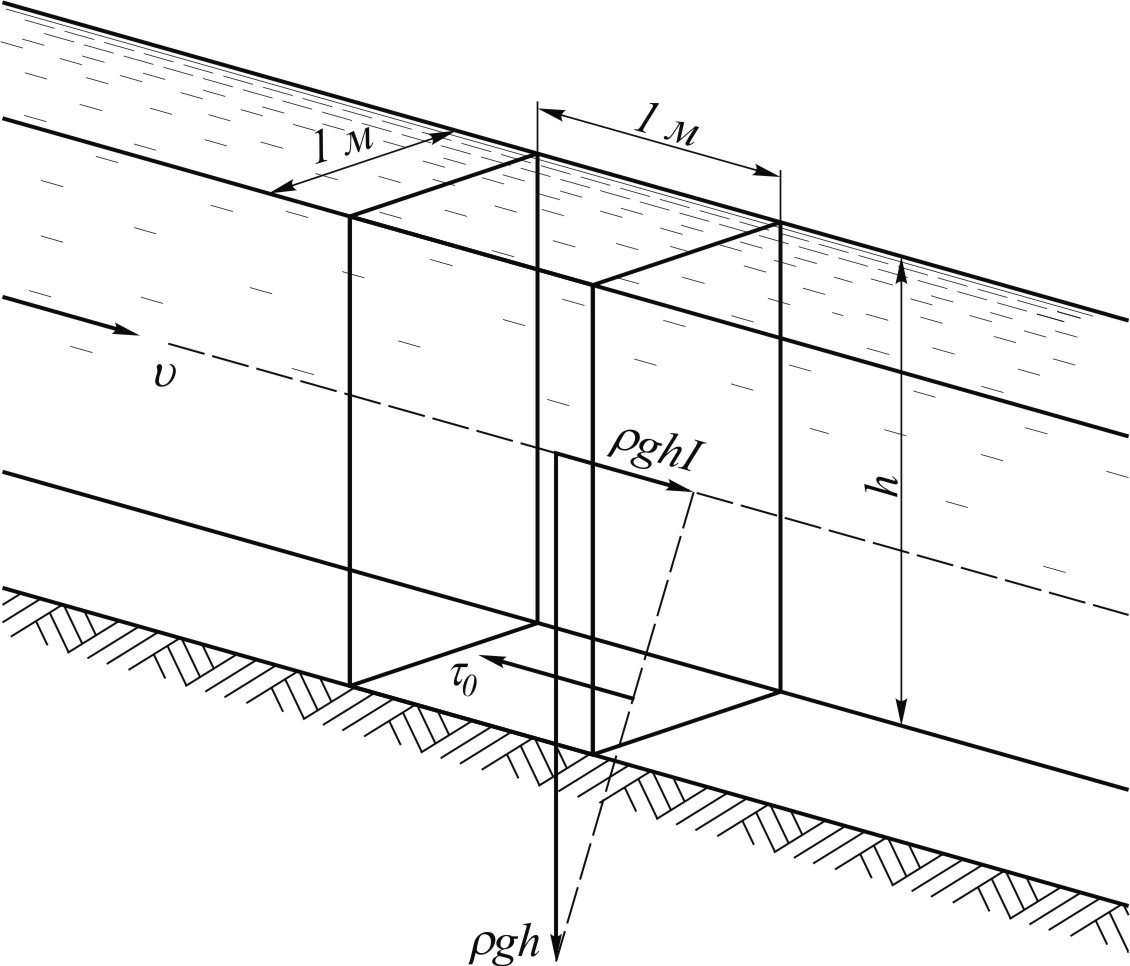
Рис. 21. Схема, иллюстрирующая уравнение равномерного движения

Силы жидкостного трения при развитом турбулентном движении пропорциональны квадрату скорости. Эту зависимость, применительно к трению на дне, выражают формулой

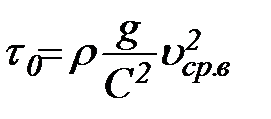, (43)

где: С – коэффициент с размерностью корня квадратного из ускорения.

Подставив выражение t₀ по (43) в уравнение (42), получим

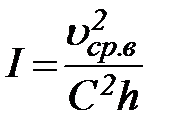(44)

Если поперечное сечение потока имеет форму широкого прямоугольника (B>>h), то скорость u_ср.в практически не отличается от средней скорости в сечении u_ср, а глубина h приближенно равна средней глубине 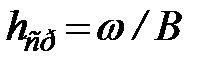. При этом формула (44) принимает вид

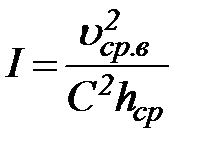. (45)

Решая равенство относительно u_ср, получаем

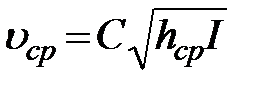. (45)

Формула (46) называется формулой Шези по имени составившего ее французского гидравлика XVIII в. А. Шези. Коэффициент С называется коэффициентом Шези. Формула (46) и эквивалентная ей формула (45) на практике применяются к поперечным сечениям любой формы, если только эта форма достаточно плавная (нет скачков глубины).

Опыт показывает, что коэффициент С является переменной величиной. Он зависит от шероховатости дна и более слабо от глубины потока. Существует ряд формул, выражающих эту зависимость. Достаточно надежна и удобна своей простотой эмпирическая формула Р. Маннинга:

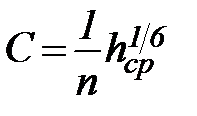(47)

где: n – коэффициент шероховатости, с/м^1/3

Значения коэффициента n для разных водоводов приводятся в гидравлических справочниках. Наиболее часто встречающиеся значения n для речных русел лежат в интервале 0,02-0,03 с/м^1/3.Коэффициенты шероховатости пойм могут достигать 0,10 с/м^1/3 и более.

Поле силы тяжести сообщает всем находящимся в нем телам определенную потенциальную энергию. Для единицы веса жидкости, движущейся в открытом русле, эта энергия равна высоте свободной поверхности над выбранной плоскостью сравнения. Преодолевая силы трения, поток тратит свою энергию, что выражается в понижении высот свободной поверхности вниз по течению. Поэтому уклон, определяемый формулой (45), называют уклоном трения, или также градиентом потерь энергии. В равномерном потоке, вдоль которого кинетическая энергия жидкости не меняется, понижение свободной поверхности полностью обусловлено потерями энергии. Это значит, что в равномерном потоке уклон трения и уклон свободной поверхности (а также уклон дна) совпадают. При неравномерном движении уклон трения может быть меньше и больше уклона свободной поверхности, в зависимости от того как меняется вдоль потока кинетическая энергия жидкости – растет она или падает.

Краткое разъяснение требуется в связи с выражением «потери энергии». Теряемая движущейся жидкостью механическая энергия переходит в тепло. Так как уклоны естественных потоков малы, малы и количества выделяемого тепла. У речного потока с уклоном 1·10^-4 и расходом 1000 м³/с скорость производства тепловой энергии на единице длины пути составляет

.

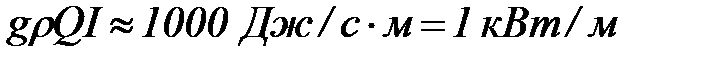Это тепло мы не замечаем. Однако если мы сконцентрируем энергию потока – построим плотину и при ней водохранилище длиной 100 км, то благодаря тому, что потери энергии в водохранилище близки к нулю, мы освободим мощность 100 тыс. кВт, которую можно использовать для получения электроэнергии.