Связь между расходом и уровнем воды

Изменение расхода воды в реке вызывает изменения всех гидравлических элементов потока: глубины и ширины живых сечений, скорости течения, коэффициента Шези и коэффициента шероховатости. Меняются и местные уклоны свободной поверхности. Пока поток не вышел на пойму, остается практически неизменным средний уклон на участках большой длины (измеряемой сотнями ширин русла), так как он не может существенно отклониться от среднего уклона дна реки. Однако при затоплении и опорожнении поймы наблюдаются изменения уклонов свободной поверхности, охватывающие участки и очень большого протяжения.

Опираясь на уравнения неустановившегося движения, автор показал, что в прямолинейных плесовых лощинах корытообразной формы (т.е. с мало изменяющейся во времени шириной) средняя глубина сечений меняется при колебаниях расхода воды по следующему приближенному закону:

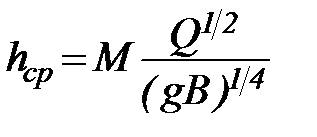, (48)

где М – безразмерная постоянная, значения которой зависят от характера грунтов дна.

Решая равенство (48) относительно расхода воды, получаем

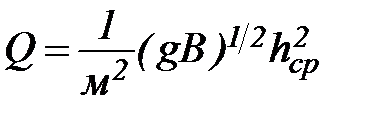. (49)

Разделов обе части уравнения (49) на площадь сечения w = Bh_сp, найдем закон изменения скорости течения:

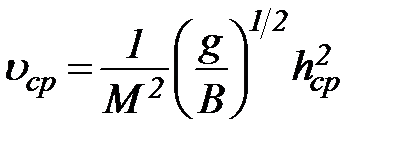. (50)

Если подставить сюда величину v_ср по формуле Шези, получится закон изменения коэффициента Шези:

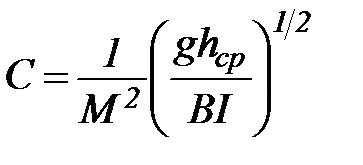. (51)

При незатопляемых берегах приближенные формулы (48) – (51) действительны во всей амплитуде колебания уровней, а при затопляемых – до выхода реки на пойму. Гидрометрические створы, в которых ведутся систематические измерения расходов воды, располагаются обычно в прямых, корытообразных плесовых лощинах. Измерения на таких створах хорошо подтверждают равенство (48). Значения постоянной М могут меняться от створа к створу, но их колебания не очень велики. Средние значения М равны: в плесовых лощинах с песчаным дном 0,9, с гравелистым дном 0,75 и с галечным 0,6.

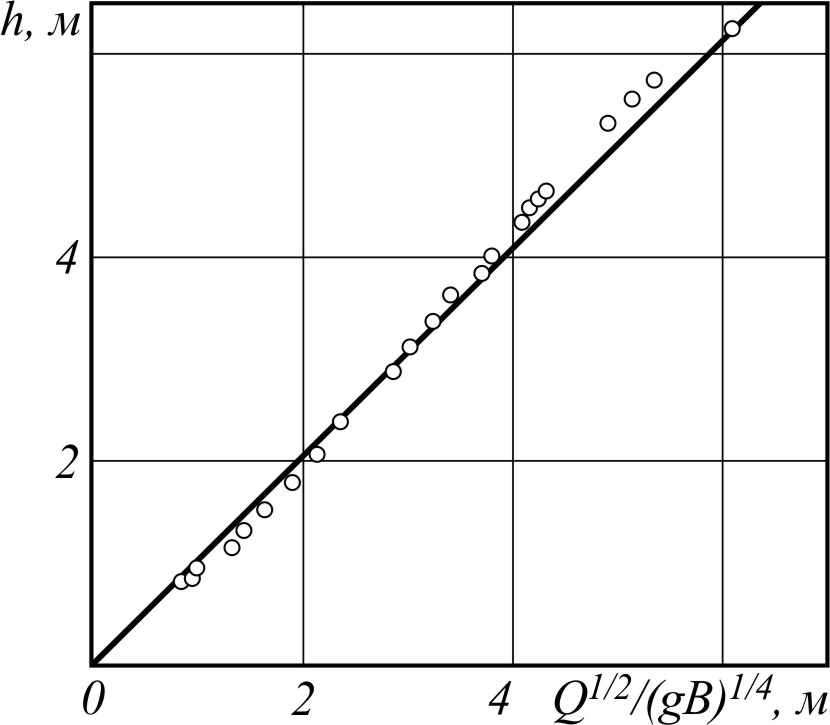Рис.22. График функции (48) для гидроствора Устюжна на р. Мологе

На рис. 22 показан график функции (48), построенный по данным измерений на гидростворе Устюжна реки Мологи. Постоянная М для этого створа равна 1,00.

Получаемая в результате измерений графическая зависимость расхода воды от уровня Q = Q(z) называется кривой расходов. Формула (49) представляет собой общую теоретическую основу всех таких кривых. Чтобы перейти от этой формулы к кривой расходов, достаточно ввести в нее связи средней глубины и ширины сечения с уровнем воды: 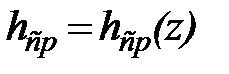и 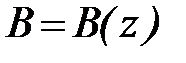. Эти связи легко построить, располагая поперечным профилем русла.

В руслах корытообразной формы связь 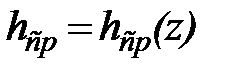близка к линейной, а ширина В меняется с уровнем слабо. Отсюда, воспользовавшись формулой (49), можно написать приближенно

.

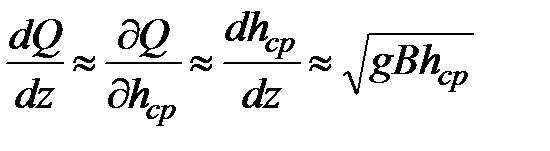Таким образом, с ростом уровня расход растет все быстрее. Все кривые расходов обращены выпуклостью к оси z. Формула (50) показывает, что рост скорости с ростом уровня замедляется.

Различные местные условия движения воды в естественных руслах могут нарушать однозначность связи между расходом и уровнем, делая зависимость (49) недействительной. Чаще всего нарушения однозначности обусловливаются деформациями русла или явлениями подпора. Если русло на участке измерения расходов размывается, то это вызывает снижение высот и у свободной поверхности. По мере размыва дна одному и тому же расходу отвечают все более низкие уровни. При намыве дна картина обратная – одному и тому же расходу начинают отвечать все более высокие уровни.

Подпор часто наблюдается выше мест слияния реки с ее притоками. Если на главной реке произошло увеличение расхода и соответственно повысились уровни, а на притоке расход не изменился, приустьевой участок последнего окажется в подпоре. Повышения расхода и уровня, происшедшие на крупном притоке, могут создать местный подпор на главной реке. Па участке подпора при неизменившемся расходе уровни повышаются, а скорости течения падают.

Радикальные изменения вносятся в связи между расходом и уровнем при появлении на реке ледяного покрова. Ледяной покров, а также скопления внутриводного льда сильно увеличивают гидравлическое сопротивление русла.

Вызываемое добавочным сопротивлением уменьшение скоростей означает увеличение площадей живых сечений. При неизменившемся расходе сразу после установления ледяного покрова уровни в реке повышаются. Если бы шероховатость нижней поверхности льда в течение зимы не изменялась и внутриводный лед отсутствовал, то мы имели бы однозначные зимние кривые расходов, смещенные по отношению к летним кривым в сторону более высоких уровней. В действительности дело обстоит не так. Шероховатость нижней поверхности льда не остается неизменной, а внутриводный лед в начале ледостава встречается почти повсеместно. Поэтому связи Q и z при ледоставе, как правило, неоднозначны.

Вопросы построения кривых расходов по данным измерений, включая вопрос о подсчетах зимнего стока, освещаются в гл. XII.