Максимальные расходы воды
Понятие максимального расхода, формирование половодий и паводков. Под максимальным расходом понимается наибольший мгновенный расход воды, прошедший через данное сечение речного русла (гидроствор) в границах года. За многолетний период ежегодные максимальные расходы образуют последовательность случайных величин, аналогичную последовательности среднегодовых расходов.
Значения максимальных расходов малой обеспеченности (малой вероятности превышения) используются для выбора размеров водопропускных отверстий плотин, а также размеров подмостовых отверстий при переходах через реки железных и автомобильных дорог. Поэтому знание таких расходов практически очень важно. Занижение расчетного расхода в проекте плотины может привести к ее разрушению, и если напор на плотине велик, то к катастрофическим последствиям на нижележащем участке реки – разрушению зданий и сооружений, расположенных на берегах, и гибели людей. Чтобы исключить такие возможности, при проектировании крупных гидроузлов в качестве расчетных принимаются максимальные расходы очень малой обеспеченности. Значения этой обеспеченности для постоянных гидротехнических сооружений четырех классов капитальности приведены в табл. 4. Все плотины, подпирающие водохранилища на больших равнинных реках СССР, относятся к первому классу капитальности.
Таблица 4
Значения обеспеченности максимальных расходов,
принимаемые в проектах гидротехнических сооружения
| Класс капитальности | Обеспеченность, %, при условиях | |
| нормальных | чрезвычайных | |
| I | 0.1 | 0.01 |
| II | 1.0 | 0.1 |
| III | 2.0 | 0.5 |
| IV | 5.0 | 1.0 |
На реках европейской территории Союза и Западной Сибири половодья, при которых наблюдаются максимальные расходы, формируются в результате весеннего снеготаяния. Некоторую, обычно небольшую, роль могут играть при их формировании и дождевые осадки. На реках Дальнего Востока половодья, как уже было сказано, формируются муссонными дождями. На малых реках, в особенности горных, максимальные расходы могут создаваться ливнями.
Формирование половодья или паводка представляет собой сложный процесс. В каждый момент времени через замыкающий гидроствор протекает вода, пришедшая сюда из разных частей бассейна. На каждом элементе площади бассейна можно определить интенсивность водоотдачи или просто водоотдачу, под которой понимается объем воды, стекающей в единицу времени с единицы площади. Водоотдача имеет размерность скорости и обычно выражается так: мм/ч или мм/сут. При снеговом половодье водоотдача равна водоотдаче тающего снегового покрова за вычетом скорости просачивания воды в грунт и скорости испарения. При дождевом паводке место водоотдачи снегового покрова занимает интенсивность выпадения жидких осадков. Для того чтобы достигнуть замыкающего створа, вода, образовавшаяся на элементарной площадке, должна затратить определенное время, называемое временем добегания. В течение половодья время добегания несколько меняется – вначале вследствие роста скоростей склонового и руслового стока убывает, затем по мере уменьшения скоростей возрастает. Для упрощения картины допустимо этими изменениями пренебречь и сопоставить каждому элементу площади бассейна постоянное время добегания. Это значит, что время добегания становится однозначной функцией географических координат. Для ее наглядного изображения на карте бассейна проводят линии равного времени добегания – изохроны. На рис. 20 такие линии отмечены значениями времени добегания t1, t2, t3, t4.
Вооружившись понятиями водоотдачи и времени добегания, можно выразить мгновенный расход воды в замыкающем створе через параметры стока с поверхности бассейна. Для этого поступим следующим образом. Пренебрегая кривизной земной поверхности, т.е. считая бассейн не очень большим, введем на его площади плоскую систему прямоугольных декартовых координат х, у. При этом водоотдача А и время добегания t выразятся функциями:
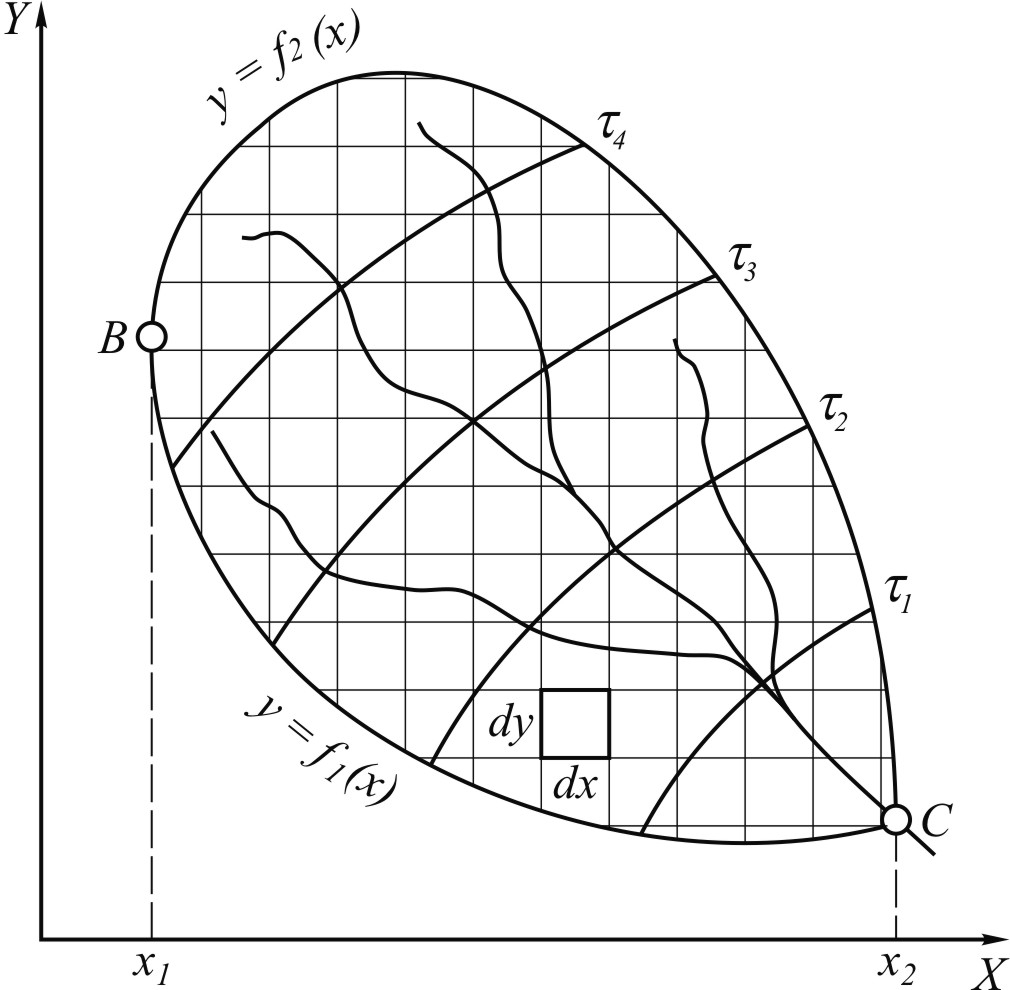 Рис.20. Схема речного бассейна
с изохронами
Рис.20. Схема речного бассейна
с изохронами
|
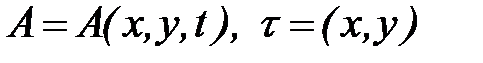 (34)
(34)
Разобьем площадь бассейна координатными линиями на элементарные прямоугольники. Абсциссы крайних точек границы бассейна В и С обозначим x1 и х2 (см. рис. 20). Линию границы бассейна, лежащую ниже прямой ВС, выразим функцией 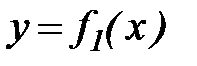 и линию границы, лежащую выше прямой ВС, – функцией
и линию границы, лежащую выше прямой ВС, – функцией 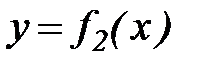 . Считая, что приток грунтовых вод в русло отсутствует[3], будем иметь следующее выражение расхода воды в замыкающем створе в произвольный момент времени t:
. Считая, что приток грунтовых вод в русло отсутствует[3], будем иметь следующее выражение расхода воды в замыкающем створе в произвольный момент времени t:
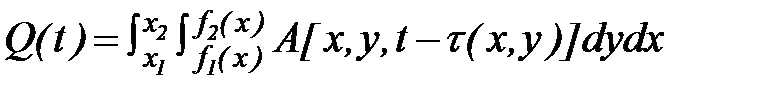 (35)
(35)
Подынтегральная функция в формуле (35) выражает водоотдачу с элементарной площадки в момент времени, удаленный назад по сравнению с моментом t на величину времени добегания.
Использовать формулу (35) для расчета максимальных расходов нельзя, так как детальной информацией об изменении водоотдачи по площади бассейна за время половодья никогда не располагают. Однако эта формула дает принципиальную основу для построения так называемых генетических формул максимальных расходов (о которых речь будет идти дальше).
Расчет максимальных расходов при наличии многолетних наблюдений. Чтобы получить значения максимальных расходов малой обеспеченности, необходимо располагать теоретической кривой обеспеченности. Основу для ее построения могут дать наблюдения над стоком, если охваченный ими ряд лет достаточно велик. Для бассейнов лесотундровой и лесной зон считается достаточным ряд в 25 лет, для бассейнов лесостепной и степной зон – 30 и 40 лет соответственно.
Теоретическая кривая обеспеченности максимальных расходов строится таким же путем, как для среднегодовых расходов. Применяется то же распределение Пирсона III типа. Сначала вычисляют среднее арифметическое значение ежегодных максимальных расходов, затем находят значения коэффициентов вариации и асимметрии и, наконец, используют таблицу Фостера-Рыбкина. Для максимумов снеговых половодий коэффициент асимметрий находят по соотношению 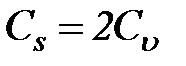 . Максимумы дождевых паводков отличаются существенно большей положительной асимметрией распределения вероятностей – высота отдельных редко повторяющихся дождевых паводков может очень сильно превосходить среднюю. Поэтому значение коэффициента асимметрии при расчете дождевых максимумов берется равным
. Максимумы дождевых паводков отличаются существенно большей положительной асимметрией распределения вероятностей – высота отдельных редко повторяющихся дождевых паводков может очень сильно превосходить среднюю. Поэтому значение коэффициента асимметрии при расчете дождевых максимумов берется равным 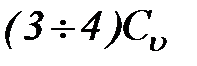 . В обоих случаях приемлемость принятых значений Cs проверяют и, если нужно, корректируют посредством совмещения с теоретической кривой точек эмпирической обеспеченности. Последнюю вычисляют по формуле (31).
. В обоих случаях приемлемость принятых значений Cs проверяют и, если нужно, корректируют посредством совмещения с теоретической кривой точек эмпирической обеспеченности. Последнюю вычисляют по формуле (31).
Описанная процедура несколько усложняется, когда цель расчетов состоит в определении максимального расхода для чрезвычайных условий эксплуатации гидротехнического сооружения. Ответственность этого случая заставляет добавлять к расходу Qmax, р, определенному по теоретической кривой обеспеченности, так называемую гарантийную поправку DQmax. Смысл этой поправки состоит в том, что исходный многолетний ряд наблюдений случайно может содержать лишь относительно невысокие максимальные расходы и вследствие этого подсчитанное значение Cu,
а с ним и значение Cs могут быть заниженными. Введение гарантийной поправки страхует от последствий такого занижения.
Величина гарантийной поправки вычисляется по формуле
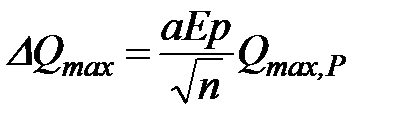 , (36)
, (36)
где: а – коэффициент «незнания» (принимаемый равным 0,7 для хорошо гидрологически изученных районов и равным 1,5 для слабо изученных);
ЕP – относительная средняя квадратичная ошибка ординат кривой обеспеченности;
n – число лет наблюдений;
Qmax, P – максимальный расход с обеспеченностью Р по теоретической кривой.
Значения ошибки ЕP зависят от коэффициента вариации максимальных расходов и расчетной обеспеченности Р. Эти значения для Р=0,01% и 0,1% приведены в табл. 5.
Расчетные максимальные расходы для чрезвычайных условий эксплуатации определяются равенством
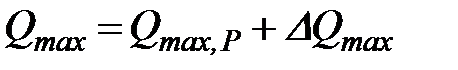 . (37)
. (37)
На такие расходы проверяется расчетом работа водопропускных отверстий плотин. Размеры отверстий выбираются из условия нормальной эксплуатации.
Расчет максимальных расходов при недостатке и отсутствии наблюдений. Если ряд наблюдений над стоком недостаточен для надежного определения параметров распределения вероятностей максимальных расходов, то прибегают к продлению ряда с помощью бассейна-аналога. Последний должен иметь условия формирования половодий, близкие к условиям в интересующем нас бассейне, и по нему должны существовать многолетние данные о стоке. Площади двух бассейнов не должны отличаться более чем в 5 раз. Процедура расчетов такая же, как при продлении ряда среднегодовых расходов (см. п. 10). Применение этого способа ограничено равнинными реками со снеговым половодьем, так как только в этом случае удается подобрать удовлетворительный бассейн-аналог и получить надежный график связи максимальных расходов.
При полном отсутствии наблюдений максимальные расходы воды вычисляют по эмпирическим формулам, в основе которых лежит генетическая связь между расходами воды в замыкающем створе и водоотдачей с поверхности бассейна. Общий вид этой связи выражается уравнением (35). Для максимумов талых вод формулы такого рода были предложены Д.И. Кочериным, Д.Л. Соколовским, Г.А. Алексеевым, К.П. Воскресенским и другими авторами. В настоящее время расчет максимальных расходов талых вод производят по указаниям СН 435-72.
Таблица 5
| Сu | P, % | Сu | P, % | Сu | P, % | |||
| 0.1 | 0.01 | 0.1 | 0.01 | 0.1 | 0.01 | |||
| 0.1 | 0.23 | 0.25 | 0.6 | 1.03 | 1.12 | 1.1 | 1.74 | 1.90 |
| 0.2 | 0.42 | 0.46 | 0.7 | 1.16 | 1.26 | 1.2 | 1.89 | 2.07 |
| 0.3 | 0.58 | 0.64 | 0.8 | 1.30 | 1.40 | 1.3 | 2.03 | 2.23 |
| 0.4 | 0.74 | 0.80 | 0.9 | 1.45 | 1.55 | 1.4 | 2.18 | 2.40 |
| 0.5 | 0.88 | 0.96 | 1.0 | 1.58 | 1.70 | 1.5 | 2.23 | 2.57 |
Рекомендуемая этими нормами основная расчетная формула близка к формуле, предложенной в 1937 г. Д.Л. Соколовским. Для равнинных бассейнов с площадью более 10 км2 она записывается в виде
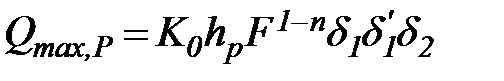 (38)
(38)
где: К0 – коэффициент дружности половодья;
hP – слой суммарного стока за время половодья, имеющий ту же обеспеченность Р, что максимальный расход, мм;
F – площадь бассейна, км2.
Коэффициенты, обозначенные буквой d, учитывают снижение максимального расхода за счет регулирующего влияния озер (d1), водохранилищ (d'1), болот и лесов (d2). Показатель степени 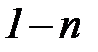 при площади бассейна принимается равным: в лесотундровой и лесной зонах и Восточной Сибири 0,83, в лесостепной и степной зонах ETC и в Западной Сибири 0,75, в западном и центральном Казахстане 0,65. Тот факт, что максимальный расход пропорционален площади бассейна в степени, меньшей единицы, объясняется тем, что рост этой площади ведет к сглаживанию неравномерности распределения водоотдачи по площади бассейна и увеличивает время добегания. Коэффициент дружности половодья К0 имеет порядок 10-2. Подробные указания об определении коэффициентов К0, d1, d'1, и d2 приводятся в СН 435-72.
при площади бассейна принимается равным: в лесотундровой и лесной зонах и Восточной Сибири 0,83, в лесостепной и степной зонах ETC и в Западной Сибири 0,75, в западном и центральном Казахстане 0,65. Тот факт, что максимальный расход пропорционален площади бассейна в степени, меньшей единицы, объясняется тем, что рост этой площади ведет к сглаживанию неравномерности распределения водоотдачи по площади бассейна и увеличивает время добегания. Коэффициент дружности половодья К0 имеет порядок 10-2. Подробные указания об определении коэффициентов К0, d1, d'1, и d2 приводятся в СН 435-72.
Так как максимальные расходы ливневого происхождения встречаются в равнинной части СССР лишь на малых реках, с площадью водосбора менее 100 км2, то на способах их расчета здесь нет необходимости останавливаться. Расчеты максимального стока на реках с муссонным и ледниковым питанием разработаны слабо.
Дата добавления: 2017-04-05; просмотров: 3246;











