Уравнение движения сплошной среды в напряжениях
Рассмотрим элементарный параллелепипед с ребрами 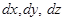 . Объем его
. Объем его 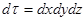 . На него действуют массовые и поверхностные силы определяемые главным вектором внешних сил
. На него действуют массовые и поверхностные силы определяемые главным вектором внешних сил 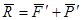 . К параллелепипеду применим закон сохранения количества движения:
. К параллелепипеду применим закон сохранения количества движения:
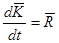
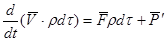

Для определения главного вектора поверхностных сил рассмотрим все силы, дающие проекцию на ось х. Для граней перпендикулярных х проекцию дают только силы, создаваемые нормальными напряжениями. Поэтому равнодействующая этих сил равна:
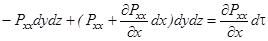
Аналогично для граней перпендикулярных z получим равнодействующую равную:
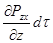
Равнодействующая поверхностных сил в проекции на ось х равна:
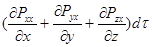
Тогда закон сохранения количества движения в проекции на х можно записать:
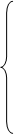

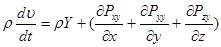
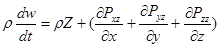
Полученная система называется системой уравнений движения сплошной среды в напряжениях. В левой части стоит полная производная от скоростей, которые могут быть расписаны через локальные и конвективные составляющие ускорения. При определенных условиях левая часть значительно упрощается (стационарное, двухмерное или одномерное течение).
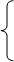 Т.к.
Т.к. 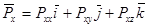
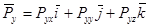
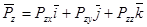
систему можно записать в виде одного уравнения в векторной форме записи:
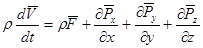
Дата добавления: 2017-04-05; просмотров: 1794;











