Частные случаи плоских потенциальных течений

1. Плоско параллельный поток:

Рассмотрим комплексный потенциал - , где а – действительное число

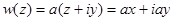и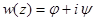

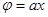- семейство прямых, параллельных оси у. 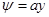- уравнение функции тока.

Линии тока 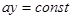- семейство прямых, параллельных оси х. 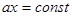- уравнение эквипотенциальных поверхностей.

Для построения поля скоростей возьмем производные

;

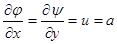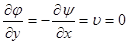
Таким образом, рассмотренный потенциал описывает плоское течение потока вдоль оси х. Величину а можно рассматривать как скорость внешнего (набегающего) потока, .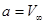

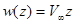
2. Источник и сток.

Рассмотрим комплексный потенциал 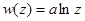, а – действительное число ( 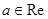), тогда

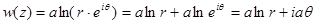
Уравнение для потенциала: 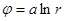. 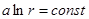- эквипотенциальные линии, семейство окружностей с центром в точке (0,0).

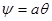- уравнение функций тока. 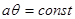- семейство прямых, проходящих через точку (0,0).

Характер (вид) течения определяет знак при а. Если a>0, то это источник, если a<0, то это – сток.

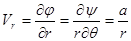
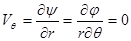
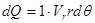- объемный расход;

;

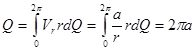
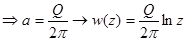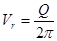
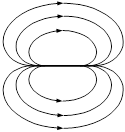
Если разместить источник и сток рядом то получится следующая картина.

Если их свести вместе, то получится диполь.

3. Рассмотрим комплексный потенциал:

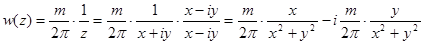
Уравнение эквипотенциальных линий 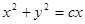- семейство окружностей, проходящих через точку (0,0) с центрами на оси х.

Уравнение для линий тока 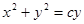- семейство окружностей, проходящих через точку (0,0) с центрами на оси у.

4. Рассмотрим комплексный потенциал вида:

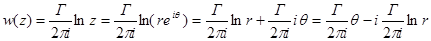
Г – циркуляция вектора скорости – круговое течение потока.

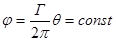- семейство прямых, проходящих через точку (0,0).

Это уравнение эквипотенциальных линий.

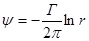- функция тока;

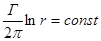- линии тока – семейство окружностей с центром в (0,0).

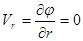- радиальная скорость;

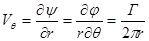
Исследованный потенциал определяет течение, которое называется потенциальным вихрем.

Окружная скорость изменяется по гиперболе.