Градиент, дивергенция, циркуляция, вихрь
1. Градиент.
Рассмотрим действие векторного оператора Гамильтона на скалярную функцию φ. Скалярная величина – это параметр, которому нельзя придать направление.
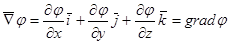
Градиент скалярной функции – это вектор направленный по нормали к линии постоянного значения в сторону возрастания функции и модуль его равен частной производной от функции по направлению указанной нормали.
2. Дивергенция.
Рассмотрим скалярное умножение векторного оператора и двух величин скорости:
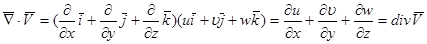
Дивергенция является скалярной величиной, показывает расхождение вектора скорости, определяет закон относительного изменения объема. Например, если течение стационарное и жидкость несжимаемая, то при 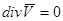 в жидкости отсутствуют источники или стоки. При
в жидкости отсутствуют источники или стоки. При 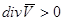 имеется источник, при
имеется источник, при 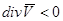 имеется сток. Уравнение
имеется сток. Уравнение 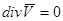 часто используется для замыкания системы уравнений движения несжимаемой жидкости и является уравнением сплошности.
часто используется для замыкания системы уравнений движения несжимаемой жидкости и является уравнением сплошности.
3. Циркуляция.
Характеризует интенсивность вращательного движения жидкости.
Вычисляется, например, по контуру АВ:
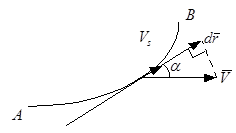
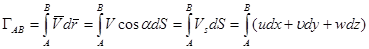
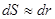
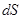 - элемент контура АВ
- элемент контура АВ
4. Вихрь вектора скорости.
Рассмотрим векторное произведение оператора на вектор скорости:
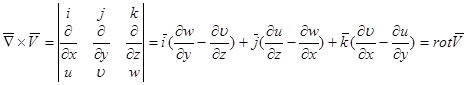

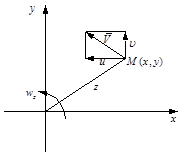
Рассмотрим вращение точки вокруг оси, проходящей через начало координат с угловой скоростью  .
.
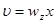
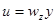
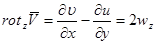
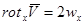
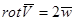
Если в жидкости  , это указывает на наличие вращающихся объемов, вихрей жидкости. Интерес представляют течения для которых
, это указывает на наличие вращающихся объемов, вихрей жидкости. Интерес представляют течения для которых 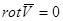 , такие течения называются безвихревыми или потенциальными,. Т.к. в этом случает существует потенциал вектора скорости φ, который связан с составляющими вектора скорости следующими соотношениями:
, такие течения называются безвихревыми или потенциальными,. Т.к. в этом случает существует потенциал вектора скорости φ, который связан с составляющими вектора скорости следующими соотношениями:
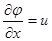 ;
; 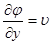 ;
; 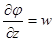 ;
; 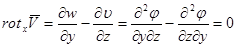
Дата добавления: 2017-04-05; просмотров: 1917;











