Маршруты в графах. Цепи. Циклы.

Определение 10.1. Маршрут – чередующаяся последовательность вершин и ребер, в которой любые два соседних элемента инцидентны.

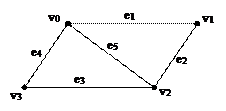m₁=v₀e₁v₁e₂v₂e₃…e_kv_k

Определение 10.2. Если v₀ = v_k, то маршрут называют цепью.

Определение 10.3. Если все вершины, а значит и ребра, различны, то маршрут называют простой цепью.

В этой цепи вершины v₀ и v_k называют концами цепи. Говорят, что цепь с концами u, v соединяет вершины u, v. Она обозначается <u, v>. Замкнутая цепь называется циклом. Замкнутая простая цепь называется простым циклом. Число циклов в графе G обозначается z(G). Граф без циклов называют ацикличным. Для орграфов цепь называется путем, а цикл – контуром.

Пример: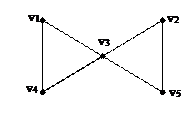

v₁v₃v₁v₄ – маршрут,

v₁v₃v₅v₂v₃v₄ – цепь,

v₁v₄v₃v₂v₅ – простая цепь,

v₁v₃v₅v₂v₃v₄v₁ – цикл,

v₁v₃v₄v₁ – простой цикл.

Длиной маршрута называется количество ребер (с повторениями).

Если маршрут m=v₀e₁v₁e₂v₂e₃…e_kv_k, то длина маршрута равна k, |m|=k, k – число ребер.

Расстояние между вершинами.

Определение 10.4. Расстояние между вершинами u и v обозначается d(u, v), называется длина кратчайшей цепи u, v. А сама кратчайшая цепь d(u, v) = min |<u, v>| называется геодезической.

Если между вершинами u, v не существует цепи, то <u, v> d(u, v) = + ∞.

Пример:

d(v₁, v₂) = + ∞.

Диаметром графа G обозначается D(G), называется длина длиннейшей геодезической, или наибольшей из кратчайших путей.

Множество вершин, находящихся на расстоянии n от вершины v (т.е. D(v, n) = {u Î U d(u, v) = n}

Связность.

Определение 10.5. Говорят, что две вершины связаны, если существует соединяющая их простая цепь.

Определение 10.6. Граф, в котором все вершины связаны – называют связным.

Отношение связанности вершин является эквивалентностью. Классы эквивалентности по отношению связанности называют компонентами связности графов. Число компонентов графа G обозначают k(G). Граф G является связным тогда и только тогда, когда k(G) = 1. Если k(G) > 1, то G – несвязный граф. Граф, состоящий только из изолированных вершин, в котором k(G) = p(G) и r(G) = 0 называют вполне несвязным графом.