Декартово произведение графов.
Пусть G1(X,E1) и G2(Y,E2) — два графа.
Определение 11.6. Декартовым произведением G1(X,E1)´G2(Y,E2) графов G1(X,E1) и G2(X,E2) называется граф с множеством вершин X´Y, в котором дуга (ребро), идущая из вершины (xiyj) в (xkyl), существует тогда и только тогда когда существует дуга (xixk), принадлежащая множеству дуг E1 и j = l или когда существует дуга (yj,yl), принадлежащая множеству E2 и i = k.
Выполнение операции декартова произведения рассмотрим на примере графов, изображенных на рис. 4. Множество вершин Z результирующего графа определяется как декартово произведение множеств X´Y. Множество Z содержит следующие элементы: z1=(x1y1), z2=(x1y2), z3=(x1y3), z4=(x2y1), z5=(x2y2), z6=(x2y3).
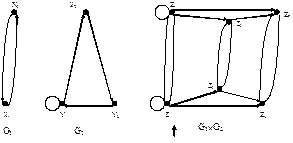
Рисунок 11.4.
Определим множество дуг результирующего графа. Для этого выделим группы вершин множества Z, компоненты которых совпадают. В рассматриваемом примере пять таких групп: две группы с совпадающими компонентами из множества X, и три группы, имеющие совпадающие компоненты из Y. Рассмотрим группу вершин результирующего графа, которые имеют общую компоненту x1: z1=(x1y1), z2=(x1y1), z3=(x1y3). Согласно определению операции декартова произведения графов, множество дуг между этими вершинами определяется связями между вершинами множества Y. Таким образом, дуга (y1,y1) в графе G2 определяет наличие дуги (z1,z1) в результирующем графе. Для удобства рассмотрения всех дуг результирующего графа составим таблицу, в первом столбце которой перечисляются вершины с совпадающими компонентами, во втором – дуги между несовпадающими компонентами, а в третьем и четвертом – дуги в результирующем графе.
| № п.п. | Группы вершин с совпадающими компонентами | Дуги для несовпадающих компонент | Дуга (xiyj)®(xkyl) | Дуга (za,zb) |
| z1=(x1y1), z2=(x1y2), z3=(x1y3) | (y1,y1) (y1,y2) (y2,y3) (y3,y1) | (x1y1)®(x1y1) (x1y1)®(x1y2) (x1y2)®(x1y3) (x1y3)®(x1y1) | (z1,z1) (z1,z2) (z2,z3) (z3,z1) | |
| z4=(x2y1), z5=(x2y2), z6=(x2y3) | (y1,y1) (y1,y2) (y2,y3) (y3,y1) | (x2y1)®(x2y1) (x2y1)®(x2y2) (x2y2)®(x2y3) (x2y3)®(x2y1) | (z4,z4) (z4,z5) (z5,z6) (z6,z4) | |
| z1=(x1y1), z4=(x2y1) | (x1,x2) (x2,x1) | (x1y1)®(x2y1) (x2y1)®(x1y1) | (z1,z4) (z4,z1) | |
| z2=(x1y2), z5=(x2y2) | (x1,x2) (x2,x1) | (x1y2)®(x2y2) (x1y2)®(x1y2) | (z2,z5) (z5,z2) | |
| Z3=(x1y3), z6=(x2y3) | (x1,x2) (x2,x1) | (x1y3)®(x2y3) (x2y3)®(x1y3) | (z3,z6) (z6,z3) |
Граф G1´ G2 изображен на рис. 11.4.
Операция декартова произведения обладает следующими свойствами.
1. G1´G2 = G2´G1
2. G1´(G2´G3) = (G1´G2)´G3.
Операция декартова произведения графов может быть выполнена в матричной форме. Пусть G1(X,E1) и G2(Y,E2) – два графа, имеющие nx и ny вершин соответственно. Результирующий граф G1´G2 имеет nx×ny вершин, а его матрица смежности вершин - квадратная матрица размером (nx×ny)´ (nx ×ny). Обозначим через aab = a(ij)(kl) элемент матрицы смежности вершин, указывающий на наличие дуги (ребра), соединяющей вершину za=(xiyj) c zb=(xkyl). Согласно определению операции этот элемент может быть вычислен при помощи матриц смежности вершин исходных графов следующим образом:
aab = a(ij)(kl) = Kik×a2,jl Ú Kjl×a1,ik, (2)
где a1,ik, a2,jl – элементы матрицы смежности вершин графов G1 и G2 соответственно;
Kik – символ Кронекера, равный 1, если i=k, и нулю, если i¹k .
Пример. Выполнить операцию декартова произведения на графах, приведенных на рис. 4.
Составим матрицы смежности вершин исходных графов.
| x1 | x2 | y1 | y2 | y3 | |||||||
| x1 | y1 | ||||||||||
| A1 | = | x2 | A2 | = | y2 | ||||||
| y3 | |||||||||||
Для построения матрицы смежности результирующего графа воспользуемся соотношением (2). В этом соотношении первое слагаемое Kik×a2,jl указывает на наличие дуг для вершин, у которых совпадают компоненты из множества X. Для пояснения сказанного, рассмотрим вспомогательную матрицу Axy, в которой элементы, для которых Kik = 1, помечены символом X. Эти элементы принимают значения, равные значениям соответствующих элементов матрицы A2 смежности вершин графа G2, так, как это показано для матрицы A*.
| x1y1 | x1y2 | x1y3 | x2y1 | x2y2 | x2y3 | |||
| x1y1 | XÚY | X | X | Y | ||||
| x1y2 | X | XÚY | X | 0 | Y | 0 | ||
| Axy | = | X1y3 | X | X | XÚY | 0 | 0 | Y |
| X2y1 | Y | 0 | 0 | XÚY | X | X | ||
| X2y2 | 0 | Y | 0 | X | XÚY | X | ||
| X2y3 | 0 | 0 | Y | X | X | XÚY |
| x1y1 | x1y2 | x1y3 | x2y1 | x2y2 | x2y3 | |||
| x1y1 | a1,11Úa2,11 | a2,12 | a2,13 | a1,12 | ||||
| x1y2 | a2,21 | a1,11Úa2,22 | a2,11 | a1,12 | ||||
| A* | = | x1y3 | a2,31 | A2,32 | a1,11Úa2,33 | 0 | 0 | a1,12 |
| x2y1 | a1,21 | 0 | 0 | a1,22Úa2,11 | a2,12 | a2,13 | ||
| x2y2 | 0 | a1,21 | 0 | a2,21 | a1,22Úa2,22 | a2,23 | ||
| x2y3 | 0 | 0 | a1,21 | a2,31 | a2,32 | a1,22Ú a2,33 |
Второе слагаемое Kjl×a1,ik соотношения(2) указывает на наличие дуг для групп вершин, у которых совпадают компоненты из множества Y. В матрице Axy элементы, для которых Kjl = 1 помечены символом Y. Эти элементы принимают значения, равные значениям соответствующих элементов матрицы A1 смежности вершин графа G1, так, как это показано для матрицы A*.
Заметим, что в матрицах Axy и A* на главной диагонали располагаются элементы, равные логической сумме значений элементов матриц смежности вершин обоих графов. Это определяется тем, что на главной диагонали расположены элементы, для которых Kik = Kjl = 1.
Таким образом, матрица смежности вершин результирующего графа принимает вид:
| x1y1 | x1y2 | x1y3 | x2y1 | x2y2 | x2y3 | |||
| x1y1 | ||||||||
| x1y2 | ||||||||
| A | = | x1y3 | ||||||
| x2y1 | ||||||||
| x2y2 | ||||||||
| x2y3 |
Нетрудно убедиться, что полученной матрице смежности вершин соответствует граф G1´G2, представленный на рис. 4
Дата добавления: 2021-07-22; просмотров: 860;











