Элементы графов. Подграфы. Валентность.

После рассмотрения определений, относящихся к графам как к цельным объектам, естественно дать определения различным составным элементам графов.

Определение 9.6. Граф G'(V', Е') называется подграфом графа G(V, Е) (обозначается G'), если V' включенов V и/или Е' включенов Е.

Определение 9.7. Если V' = V, то G' называется остовным подграфом G.

Определение 9.8. Если V' включенов V и Е' включенов Е (причем V' не равно V и E' не равно E ), то граф G' называется собственным подграфом графа G.

Определение 9.9. Подграф G'(V',Е') называется правильным подграфом графа G(V,Е), если G' содержит все возможные ребра G. Правильный подграф G'(V, Е') графа G(V, Е) определяется подмножеством вершин V'.

Определение 9.10. Количество ребер, инцидентных вершине v, называется степенью (или валентностью вершины v) и обозначается d(v).

Причем 0 £ d(v) £1 d(v) = |Г(v)|.

Обозначим минимальную степень вершины графа G через d(G), а максимальную — через D(G).

Определение 9.11. Если степени всех вершин равны k, то граф называется регулярным степени k:

Степень регулярности является инвариантом графа и обозначается r(G). Для нерегулярных графов r(G) не определено.

Пример:Ниже приведена диаграмма регулярного графа степени 3

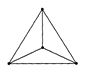
Если степень вершины равна 0, то вершина называется изолированной. Если степень вершины равна 1, то вершина называется концевой, или висячей.

Для орграфа число дуг, исходящих из вершины v, называется полустепенъю исхода, а входящих – полустепенью захода. Обозначаются эти числа, соответственно, d^–(v) и d⁺(v).

Теорема Эйлера.

Теорема Эйлера:Сумма степеней вершин графа равна удвоенному количеству ребер: .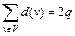

Для ориентированного графа: .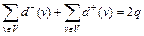

Доказательство:При подсчете суммы степеней вершин каждое ребро учитывается два раза для одного конца ребра и для другого.