Основное определение.
Среди дисциплин и методов дискретной математики теория графов и особенно алгоритмы на графах находят наиболее широкое применение в программировании
Теория графов многократно переоткрывалась разными авторами при решении различных прикладных задач.
1. Задача о Кенигсбергских мостах. Обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку (рис. 9.1(а)). Эта задача была решена Эйлером (1707-1783) в 1736 году.
2. Задача о трех домах и трех колодцах. Имеется три дома и три колодца. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались (рис. 9.1(б)). Эта задача была решена Куратовским (1896-1979) в 1930 году.
3. Задача о четырех красках. Любую карту на плоскости раскрасить четырьмя красками так, чтобы никакие две соседние области не были закрашены одним цветом (рис. 9.1(в)).
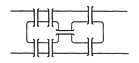
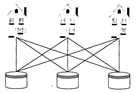
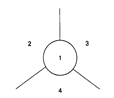
а) б) в)
Рисунок 9.1.
Определение 9.1. Графом G(V, E) называется совокупность двух множеств – непустого множества V (множества вершин) и множества E неупорядоченных пар различных элементов множества V (E – множество ребер). G(V, E)=<V, E>, V≠Æ, EÌV´V, E=E-1. Число вершин графа G обозначим р, а число ребер — q: p:=p(G):=|V|, q:=q(G):=|E|.
Определение 9.2. Пусть ν1, ν2 — вершины, e = (ν1, ν2) – соединяющее их ребро. Тогда вершина νi и ребро e инцидентны, вершина ν2 и ребро e также инцидентны. Два ребра, инцидентные одной вершине, называются смежными, две вершины, инцидентные одному ребру, также называются смежными.
Смежность.
Определение 9.3. Множество вершин, смежных с вершиной ν, называется множеством смежности вершины ν и обозначается Г+(ν): Г+(ν):={ u Î V | (u, v) Î E}, Г(ν):=Г.
Часто рассматриваются следующие родственные графам объекты: 1) Если элементами множества Е являются упорядоченные пары, то граф называется ориентированным (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества Е-дугами. 2) Если элементом множества Е может быть пара одинаковых (не различных) элементов V, то такой элемент множества Е называется петлей, а граф называется графом с петлями (или псевдографом ). 3) Если Е является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф называется мультиграфом. 4) Если элементами множества Е являются не обязательно двухэлементные, а любые подмножества множества V, то такие элементы множества Е называются гипердугами, а граф называется гиперграфом. 5)Если задана функция Р: V Þ М и/или Р: Е Þ М, то множество М называется множеством пометок, а граф называется помеченным (или нагруженным). В качестве множества пометок обычно используются буквы или целые числа.
Далее выражение "граф G{V,Е}" означает неориентированный непомеченный граф без петель и кратных ребер.
Изоморфизм графов.
Определение 9.4. Говорят, что два графа G1(V,Е) и G2(V,Е) - изоморфны (обозначается G1 ~ G2), если существует биекция Н:V1ÞV2, сохраняющая смежность e1=(u, v)ÎE1. Из этого и наличия биекции следует, что е2(h(u),h(v))ÎE2. Изоморфизм графов есть отношение эквивалентности. Действительно, изоморфизм обладает всеми необходимыми свойствами:
1) рефлексивность G1 ~ G2, где требуемая биекция есть тождественная функция,
2) симметричность если G1 ~ G2 с биекцией h, то G2 ~ G1с биекцией h-1,
3) транзитивность если G1 ~ G2с биекцией h и G2 ~ G3с биекцией g, то G1 ~ G3 с
биекцией hg.
Графы рассматриваются с точностью до изоморфизма, то есть рассматриваются классы эквивалентности по отношению изоморфизма.
Пример:
Три внешне различные диаграммы являются диаграммами одного и того же графа:
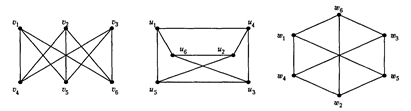
Определение 9.5. Числовая характеристика, одинаковая для всех изоморфных графов, называется инвариантом графа. Так, р(G) и q(G) — инварианты графа G. Неизвестно никакого набора инвариантов, определяющих граф с точностью до изоморфизма
Пример:
Количество вершин, ребер и количество смежных вершин для каждой вершины не определяют граф. Ниже представлены диаграммы графов, у которых указанные инварианты совпадают, но графы при этом не изоморфны
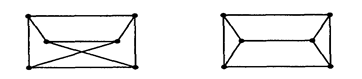
Дата добавления: 2021-07-22; просмотров: 520;











