Задача о минимальном остове
Остовом связного неориентированного графа G={V,E) называется подграф G'=(V',T) графа G, который является деревом и содержит все вершины данного графа G, то есть V-V, T 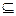 E.
E.
Поскольку остов содержит все вершины данного графа G, то в дальнейшем остов будем отождествлять с множеством его ребер Т. Из теоремы 2.1 следует, что |Т|=n-1, где n=|V|.
Задача построения остова данного графа G фактически рассматривалась ранее в главе 4. Действительно, ребра, соответствующие дугам как ПВГ-дерева, так и ПВШ-дерева, строящихся алгоритмами ПОИСК В ГЛУБИНУ и ПОИСК В ШИРИНУ, являются остовами графа G. Далее, поскольку оба алгоритма поиска имеют сложность O(n+m), и для связных графов справедливо неравенство m ≥ n-1, где n=|V|, m=|E|, то сложность поиска в связном графе есть О(m). Таким образом справедлива
Теорема 5.1.Остов связного неориентированного графа может быть построен за время О(m).
Однако, нас в этой главе будет интересовать другая, более сложная задача о построении остова.
Напомним, что граф G=(V,E) называется взвешенным, если задана функция с:E→R; иначе говоря, каждому ребру е графа G приписано число с(е). Число с(е) называется весом или стоимостью ребра е, а взвешенный граф обозначается так: G=(V,E,c).
Пусть Т — остов графа G. Число с(Т) = ∑{с(е) : е  Т} назовем весом остова Т (или стоимостью остова Т). Остов Т назовем минимальным остовом графа G, если для любого остова Т графа G справедливо неравенство с(Т)<с(Т').
Т} назовем весом остова Т (или стоимостью остова Т). Остов Т назовем минимальным остовом графа G, если для любого остова Т графа G справедливо неравенство с(Т)<с(Т').
Задача о минимальном остове формулируется следующим образом: в данном связном неориентированном взвешенном графе G построить минимальный остов.
Эта задача имеет широкое практическое применение. Предположим, например, что требуется построить сеть подачи нефти с места добычи на k перерабатывающих предприятий. Тогда минимальный остов графа, вершины которого соответствуют пунктам переработки и пункту добычи, а веса ребер — затратам на сооружение нефтепровода между соответствующими пунктами, даст наиболее экономичный способ сооружения распределительной сети.
Аналогичным образом сводится к задаче о минимальном остове, задача проектирования линий связи между некоторым центральным пунктом и периферийными пунктами.
Пусть G=(V,E,c) — заданный граф. Семейство подграфов r={Г1=(V1,Е1),...,Гк=(Vk,Еk)} графа G называется остовным лесом (или короче лесом) графа G, если
1. каждое Гр (р=1,2,...,k) является деревом;
2. Vp 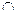 Vq=Ø (p,q=1,2,…,k);
Vq=Ø (p,q=1,2,…,k);
3. V=V1 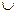 V2
V2 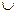 …
… 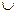 Vk.
Vk.
Иначе говоря, лес состоит из вершинно-непересекающихся деревьев. Для заданного леса r, через Еr обозначим множество ребер графа G, входящих хотя бы в одно из деревьев этого леса. Пусть Гр — дерево леса. Ребра графа G, соединяющие вершины дерева Гр с вершинами, не входящими в Гр, будем называть внешними к дереву Гр. Ребра графа G, внешние по отношению к какому-либо дереву леса r, будем называть внешними к лесу r. Понятно, что внешнее к лесу ребро является внешним к двум деревьям этого леса.
Пусть e={v,w} — внешнее к лесу r ребро, причем v  Vp, w
Vp, w  Vq, p≠q. Расширением r(e) леса r по ребру е назовем лес, полученный из r слиянием двух деревьев Гр и Гq в одно. Точнее, из леса r удаляем деревья Гр и Гq, а вместо них добавляем новое дерево (Vp
Vq, p≠q. Расширением r(e) леса r по ребру е назовем лес, полученный из r слиянием двух деревьев Гр и Гq в одно. Точнее, из леса r удаляем деревья Гр и Гq, а вместо них добавляем новое дерево (Vp 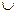 Vq,Ep
Vq,Ep 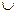 Eq
Eq 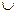 {е}). Ясно, что в лесе r(е) деревьев на единицу меньше, но ребер в Е,(е) на единицу больше (а именно, на ребро е).
{е}). Ясно, что в лесе r(е) деревьев на единицу меньше, но ребер в Е,(е) на единицу больше (а именно, на ребро е).
Пусть
c(r) = min{c(T): T 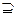 Er, Т — остов графа G},
Er, Т — остов графа G},
то есть с(r) равно минимуму весов всех остовов графа G, содержащих все ребра заданного леса r. Положим
C=min{c(T) : Т — остов графа G}.
Легко видеть, что для любого леса г справедливо неравенство с(r) ≥ С. Заметим, что если в качестве леса r выбрать тривиальный лес { ({V1 },Ø),...,({vn},Ø) }, то есть лес, в котором каждое дерево состоит ровно из одной единственной вершины, то справедливо равенство с(r)=С. Этот тривиальный лес обозначим через r0.
Оба алгоритма решения задачи о минимальном остове, которые будут здесь изложены, основаны на следующем утверждении.
Лемма 5Л.Пусть r={Г1=(V1,E1),..., Гk=(Vk,Ek)} — остовный лес графа G. Ребро e={v,w} — внешнее к лесу г ребро, причем v  Vp. w
Vp. w  Vq, p≠q и для ребра е справедливо хотя бы одно из равенств:
Vq, p≠q и для ребра е справедливо хотя бы одно из равенств:
а) либо с(е) = min{c(e*): е* —- внешнее к Гр},
б) либо с(е) = min{c(e*): е* — внешнее к Гq,}.
Тогда справедливо равенство с(r(е)) = с(r).
Справедливость неравенства с(r(е)) ≥ с(r) очевидна, ибо всякий остов, содержащий все ребра леса r(е), содержит и все ребра леса r. Докажем обратное неравенство.
Достаточно доказать, что для каждого остова Т, содержащего Е, (то есть все ребра леса r), найдется остов Т*, содержащий Еr(е), (то есть все ребра леса r(е)) такой, что с(Т*)< с(Т).
Пусть Т — остов графа G, Т 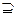 Ег и е
Ег и е 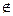 Т. Будем для определенности считать, что для ребра е справедливо первое из равенств, о которых говорится в условиях леммы. То есть с(е) = min{c(e*) : е* — внешнее к Гр}. Добавим ребро е к остову Т. По теореме 2.1 образуется ровно один цикл. Этот цикл обязательно содержит ребро e*=(v*,w*), внешнее к дереву Гр. По предположению, справедливо неравенство с(е) ≤ с(е*).
Т. Будем для определенности считать, что для ребра е справедливо первое из равенств, о которых говорится в условиях леммы. То есть с(е) = min{c(e*) : е* — внешнее к Гр}. Добавим ребро е к остову Т. По теореме 2.1 образуется ровно один цикл. Этот цикл обязательно содержит ребро e*=(v*,w*), внешнее к дереву Гр. По предположению, справедливо неравенство с(е) ≤ с(е*).
Заменим в остове Т ребро е* на ребро е. Полученный остов обозначим Т*. Так как удаленное ребро являлось внешним к лесу r, то справедливо включение Т* 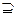 Еr, и, следовательно, Т*
Еr, и, следовательно, Т*  Еr(e). Кроме того. с(Т*)≤с(Т), так как с(е) < с(е*). Тем самым неравенство с(r(е)) < с(r) доказано, i
Еr(e). Кроме того. с(Т*)≤с(Т), так как с(е) < с(е*). Тем самым неравенство с(r(е)) < с(r) доказано, i
Доказанная лемма позволяет сконструировать два алгоритма построения минимального остова. В их основе лежит принцип пошагового наращивания остовного леса r таким образом, чтобы число с(r) не менялось.
Дадим неформальную запись этих алгоритмов.
Жадный алгоритм.
1. Лес r0 объявить растущим лесом г. (Напомним, что через r0 обозначен ранее тривиальный лес, и что с(r0) = С).
2. Пусть r — текущий растущий лес. Выбрать ребро е минимального веса среди всех внешних к r ребер. Провести расширение леса r по ребру е. Новый лес объявить растущим.
3. Осуществлять пункт 2 до тех пор, пока текущий лес не сольется в одно дерево.
В силу леммы 5.1 для каждого текущего леса r справедливо равенство с(r)=С, так как для выбираемого ребра в пункте 2 алгоритма справедливы оба равенства а) и б) леммы 5.1. Справедливость равенства с(r)=С для последнего леса, состоящего из одного единственного дерева означает, что алгоритм завершает свою работу построением минимального остова исходного графа.
Поедающий алгоритм
1. Лес r0 объявить растущим лесом r. В лесе r0 выбрать произвольное дерево (то есть вершину), которое объявить растущим деревом Г.
2. Пусть Г — растущее дерево текущего леса г. Выбрать ребро е, минимальное по весу среди всех ребер, внешних к дереву Г. Провести расширение r по ребру е. В новом лесс дерево, содержащее ребро е, объявить растущим.
3. Повторять пункт 2 до тех пор, пока растущее дерево не станет остовом (иначе говоря, до тех пор, пока оно не поглотит все остальные вершины).
Корректность поедающего алгоритма также следует из леммы 5.1. Отметим только, что здесь, в отличии от жадного алгоритма, каждый раз выполняется, вообще говоря, лишь одно из равенств а) или б) в лемме 5.1.
Перейдем к формальным описаниям изложенных способов построения минимального остова. Начнем с жадного алгоритма. Этот алгоритм впервые появился в работе Борувки, опубликованной в 1926 году. Однако, эта работа была практически забыта. Появление, а затем и широкое распространение компьютеров стимулировало интерес математиков к построению алгоритмов решения дискретных задач. В результате, в 1956 году Краскл вновь открыл жадный алгоритм. С тех пор во многих книгах (например, в [4], [6], [7]) этот жадный алгоритм называют алгоритмом Краскла. Мы будем называть его алгоритмом Борувки- Краскла.
Одной из основных операций в алгоритме Борувки-Краскла является операция слияния деревьев. Для эффективной организации этого процесса будем использовать три одномерных массива — ИМЯ, СЛЕД, РАЗМЕР, каждый длины n.
Будем считать, что в каждом дереве Г*=(У*,Е*), строящегося леса г выделена вершина v  V*, и для всех остальных вершин w
V*, и для всех остальных вершин w  V* справедливо равенство ИМЯ[w]= v. Тем самым вершины разных деревьев имеют разные имена.
V* справедливо равенство ИМЯ[w]= v. Тем самым вершины разных деревьев имеют разные имена.
Вообще говоря, одного массива ИМЯ вполне достаточно для описания множества вершин некоторого дерева, однако если ограничиваться только этим массивом, то для определения всех вершин данного дерева, входящего в лес, пришлось бы просмотреть весь массив ИМЯ. Просмотра всего массива ИМЯ можно избежать, используя массив СЛЕД, который задает «кольцевую» структуру на множествах вершин деревьев, следующим образом. Считаем, что множество вершин V* дерева Г*=(V*,Е*) упорядочено произвольным образом: V*={v1,...,vs}. Будем считать, что СЛЕД[vк]=vк+1 для всех k=l,...,s-l, и СЛЕД[vs]=v1 т.е. СЛЕД[v] дает следующую вершину множества V*, при этом первая вершина следует за последней.
Наконец, PA3MEP[v] указывает количество вершин в дереве с именем v.
Опишем теперь процедуру слияния двух деревьев Г'- (V',E') и Г"=( V",Е") по ребру {v,w}, где v  V', w
V', w  V". Считаем, что определены массивы ИМЯ, СЛЕД, РАЗМЕР и р=ИМЯ[v], q=ИМЯ[w], причем p≠q.
V". Считаем, что определены массивы ИМЯ, СЛЕД, РАЗМЕР и р=ИМЯ[v], q=ИМЯ[w], причем p≠q.
Отметим некоторые особенности работы этой процедуры. Объединение множеств V' и V" состоит в сущности в смене имени у всех вершин множества V" (цикл 4-7). Отсюда следует несимметричность процедуры, а именно, сложность выполнения процедуры СЛИТЬ(v,w,p,q) равна O(|V"|), a СЛИТЬ(w,v,q,p) — O(|V'|).
Строки 8-10 предназначены для сохранения структуры данных. В них происходит формирование одного кольцевого списка описания множества V'  V" из двух списков. Для этого достаточно исправить всего лишь две ссылки СЛЕД[v] и СЛЕД[w], и установить длину для нового кольца, получившего имя р. Множество с именем q исчезает.
V" из двух списков. Для этого достаточно исправить всего лишь две ссылки СЛЕД[v] и СЛЕД[w], и установить длину для нового кольца, получившего имя р. Множество с именем q исчезает.
Теперь у нас все готово для формализованного описания жадного алгоритма. Предполагается, что граф задан либо списками, либо массивом, либо матрицей смежностей. Отметим, что условие в строке 13 обеспечивает эффективность выполнения процедуры СЛИТЬ, так как имена меняются у того множества, которое содержит меньше элементов.
АЛГОРИТМ 5.1. БОРУВКА-КРАСКЛ
Данные: связный взвешенный граф G=(V,E,c).
Результат: Т — минимальный остов графа G.

Теорема 5.2.Вычислительная сложность алгоритма Борувки- Краскла равна O(mlogm).
Сложность формирования очереди в строке 2 есть O(mlogm) (см.гл.З). Цикл в строках 7-17 проработает в худшем случае m раз, ибо в этом случае нужно просматривать все ребра. Однако увеличение Т будет проходить ровно (n-1) раз, и каждое увеличение Т соответствует вызову процедуры СЛИТЬ. Слияние деревьев заключается в изменении переменной ИМЯ[v] для всех вершин v одного из деревьев.
Каждая вершина v  V может менять ИМЯ[v] не более
V может менять ИМЯ[v] не более 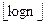 раз, ибо при каждом слиянии размер нового множества вершин не менее чем в два раза больше размера изменяемого множества (см. строки 13-14). Действительно, пусть вершина v меняет имя к раз. Обозначим через V1,V2,...,Vk=V последовательно множества вершин тех деревьев растущего леса в которые попадала вершина v. Тогда справедлива следующая цепочка равенств и неравенств:
раз, ибо при каждом слиянии размер нового множества вершин не менее чем в два раза больше размера изменяемого множества (см. строки 13-14). Действительно, пусть вершина v меняет имя к раз. Обозначим через V1,V2,...,Vk=V последовательно множества вершин тех деревьев растущего леса в которые попадала вершина v. Тогда справедлива следующая цепочка равенств и неравенств:
|V, 1=1, | V2| > 2,..., | Vi | > 2i,…,n=|V| = |vk|≥2k,
отсюда n ≥ 2k, то есть k ≤ logn.
Значит, затраты на слияние равны O(nlogn), так как в графе n вершин. Итого, сложность цикла 7-17 есть 0(m+nlogn). Окончательно, сложность алгоритма 5.1 равна
O(mlogm) + 0(m+nlogn)=0(mlogm),
ибо связность графа G влечет, что m ≥ n-l. □
 На рис.5.1 изображен связный взвешенный неориентированный граф G. Числа, стоящие рядом с ребрами, означают их веса. Минимальный остов получен в предположении, что ребра упорядочены в соответствии с их весами следующим образом: ОЧЕРЕДЬ = { {1,2},{3,4},{5,6},{1,3},{2,4},{ 1,4},{3,5},{4,6},{3,6} }. В приведенной ниже таблице показано, как формировался остов данного графа.
На рис.5.1 изображен связный взвешенный неориентированный граф G. Числа, стоящие рядом с ребрами, означают их веса. Минимальный остов получен в предположении, что ребра упорядочены в соответствии с их весами следующим образом: ОЧЕРЕДЬ = { {1,2},{3,4},{5,6},{1,3},{2,4},{ 1,4},{3,5},{4,6},{3,6} }. В приведенной ниже таблице показано, как формировался остов данного графа.

| |T| | ИМЯ | T |
| 1 2 3 4 5 6 | ||
| 1 2 3 4 5 6 | Ø | |
| 1 1 3 4 5 6 | {1,2} | |
| 1 1 3 3 5 6 | {1,2}, {3,4} | |
| 1 1 3 3 5 5 | {1,2}, {3,4}, {5,6} | |
| 1 1 1 1 5 5 | {1,2}, {3,4}, {5,6}, {1,3} | |
| 1 1 1 1 1 1 | {1,2}, {3,4}, {5,6}, {1,3}, {3,5} |
Перейдем к рассмотрению поедающего алгоритма. История его появления во многом схожа с историей предыдущего алгоритма. Впервые он появился в работе Ярника, опубликованной в 1930 году, затем переоткрыт Примом в 1957 году и, независимо, Дейкстрой в 1959 году. При этом Дейкстра предложил довольно эффективную реализацию этого алгоритма — метод расстановки специальных меток, который мы здесь будем использовать. В литературе поедающий алгоритм чаще всего называют алгоритмом Прима, реже — алгоритмом Прима-Дейкстры. Справедливее называть его алгоритмом Ярника-Прима-Дейкстры. что мы и будем делать.
Для ребра e={v,w} вместо c({v,w}) будем писать c(v,w). Напомним, что в поедающем алгоритме остовной лес расширяется путем поглощения одним и тем же деревом ближайшей к нему вершины графа. А именно, если V* — множество вершин растущего дерева, то каждый раз ищется вершина v, не входящая в V*. для которой существует вершина w из V* так, что выполняется условие
c(v,w) = min{c(u,u') : u  V*, u'
V*, u' 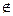 V*}.
V*}.
Понятно, что эффективность этого алгоритма зависит от того, насколько быстро будет осуществляться поиск ближайшей к растущему дереву вершины. Эффективный выбор ближайшей вершины можно осуществить с помощью двух массивов: БЛИЖНИЙ и массива меток d. Пусть V* — множество вершин растущего дерева. Через d[v] обозначим расстояние от v до множества V*, то есть
d[v] = min{c(v,u) : u  V*}.
V*}.
Значением БЛИЖНИИ[v] является та самая вершина w из V*, для которой этот минимум реализуется. Таким образом, всегда выполняется равенство
d[v] = с(v,БЛИЖНИЙ[v]).
Через F будем обозначать множество вершин, не входящих в растущее дерево. Будем считать, что если {v,w} 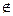 E, то c(v,w)=+∞. Через MIN(F) обозначим функцию, значением которой является вершина v
E, то c(v,w)=+∞. Через MIN(F) обозначим функцию, значением которой является вершина v  F, имеющая минимальное значение метки d. Иначе говоря, вершина MIN(F) ближе всего расположена к растущему дереву с множеством вершин V\F.
F, имеющая минимальное значение метки d. Иначе говоря, вершина MIN(F) ближе всего расположена к растущему дереву с множеством вершин V\F.
АЛГОРИТМ 5.2. ЯРНИК-ПРИМ-ДЕЙКСТРА
Данные: связный неориентированный взвешенный граф G=(V,E,c). заданный матрицей весов А[1..n].
Результат: Т — минимальный остов графа G.

Теорема 5.3.Алгоритм Ярника-Прима-Дейкстры имеет сложность O(n)
Каждый проход цикла 7-14 завершается добавлением новой вершины в растущее дерево, или, что то же самое, уменьшением на единицу числа вершин в множестве F. Отметим, что цикл 7-14 работает n-1 раз. Пусть растущее дерево содержит k вершин, тогда в F ровно n-k вершин. Следовательно, число операций, требуемых для выбора вершины MIN(F), пропорционально n-k (строка 8). В строках 10-13 осуществляется пересчет меток для n-k-1 вершины, то есть число операций в цикле 10-13 пропорционально n-k-1, или, что то же самое, пропорционально n-k. Окончательно, число операций в алгоритме 5.2 пропорционально сумме
S=n+(n-1 )+(n-2)+... +1,
которая имеет порядок n2, что доказывает теорему.
Проиллюстрируем работу алгоритма 5.2 на графе, изображенном ранее на рис.5.1. Здесь в качестве вершины w выбрана вершина с номером 1.
| |T| | V*=V\F | БЛИЖНИЙ | D | Т |
| 2 3 4 5 6 | 2 3 4 5 6 | |||
| 1 1 1 1 1 | 2 3 4 ∞ ∞ | Ø | ||
| 1,2 | 1 2 1 1 | 3 3 ∞ ∞ | {1,2} | |
| 1,2,3 | 3 3 3 | 2 4 5 | {1,2}, {1,3} | |
| 1,2,3,4 | 3 4 | 4 4 | {1,2}, {1,3}, {3,4} | |
| 1,2,3,4,5 | {1,2}, {1,3}, {3,4}, {3,5} | |||
| 1,2,3,4,5,6 | {1,2}, {1,3}, {3,4}, {3,5}, {5,6} |
В результате получим тот же остов Т, что и на рис.5.1. Здесь неявно предполагалось, что функция MIN(F) при наличии нескольких претендентов выбирает тот, у которого номер меньше. Например, в третьей строке таблицы вершине 3 отдано предпочтение перед вершиной 4. Аналогичная ситуация в предпоследней строке.
Постройте остов этого графа G в предположении, что функция MIN(F) отдает предпочтение вершинам с большими номерами.
В научной литературе имеется много работ, посвященных различным вариантам постановки задачи о минимальном остове. Например, совсем недавно разработан алгоритм построения минимального остова Евклидова графа, имеющий сложность O(nlogn). Здесь под Евклидовым графом понимается граф, вершины которого лежат в n-мерном Евклидовом пространстве, все они смежны, а вес ребра полагается равным расстоянию между его концами. Частный случай задачи о минимальном остове Евклидова графа при n=2 (случай плоскости), находит непосредственное применение в автоматическом проектировании радиоэлектронных изделий.
ЗАДАЧИ
1. Пусть во взвешенном графе G множество вершин V разбито на два непересекающихся подмножества V1 и V2, е — ребро минимального веса среди всех ребер, соединяющих вершины множеств V1 и V2. Докажите, что любой минимальный остов графа G содержит ребро, соединяющее V1 и V2, того же веса, что и у ребра е (Это утверждение иногда называют леммой Прима. По сути дела, это перефразировка леммы 5.1).
2. Предложите алгоритм построения остова максимального веса.
3. Исследовать min-max задачу построения остова. А именно. весом остова Т графа G считаем число с(Т)=mах{с(е) : е  Т}. Требуется найти остов минимального веса. Аналогично, сформулируйте и исследуйте max-min задачу построения остова.
Т}. Требуется найти остов минимального веса. Аналогично, сформулируйте и исследуйте max-min задачу построения остова.
4. Пусть в связном неориентированном графе G=(V,E) ребра разделяются на два класса: класс "плохих" и класс "хороших" ребер. Предложите алгоритм сложности О(m), строящий остов такого графа с минимально возможным количеством "плохих" ребер.
5. Пусть М — множество точек на плоскости. Рассмотрим граф, вершинами которого являются точки множества М, все они считаются смежными, а веса ребер равны расстоянию между соответствующими точками. Минимальный остов этого графа называется минимальным связывающим деревом (МСД) множества М. Предложите алгоритм построения МСД множества М сложности O(nlogn), где n=|М|.
Докажите, что степень вершины в МСД не более 6, если рассматривается евклидова метрика, и не более 8, если рассматривается прямоугольная метрика: d(x,y)= |x1—у1|+|х2—у2|.
6. Рассмотрим следующий алгоритм построения минимального остова графа G=(V,E,c).
1) Лес r0 объявить растущим лесом r.
2) Пусть r — текущий лес. Просмотреть все множество Е и зафиксировать по одному внешнему ребру минимального веса для каждого дерева из леса r (ребро — внешнее для дерева, если ровно один его конец принадлежит этому дереву).
3) Добавить выбранные ребра к лесу r. Выделить компоненты связности нового графа, полученный лес объявить растущим.
4) Повторять 2 и 3, пока лес не сольется в одно дерево.
Предложите реализацию этого алгоритма сложности 0(mlogn).
7. Транспортное управление планирует строительство дорог, которые должны соединить пять населенных пунктов. Все эти пункты должны быть соединены друг с другом либо непосредственно, либо дорогой, проходящей через другой пункт. Затраты (в млн. руб.) на строительство приводятся в таблице. Число ноль означает, что соответствующая дорога уже имеется. Какие дороги следует построить?
В пункт
| A | B | C | D | E | |
| A | — | ||||
 B B
| — | ||||
| C | — | ||||
| D | — | ||||
| E | — |
Глава VI
Пути в сетях
Напомним, что ориентированный взвешенный граф G=(V,E,c) называется сетью. Сеть может быть представлена в компьютере матрицей весов дуг, массивами смежностей СЛЕД или ПРЕДШ, или списками СЛЕД[v] или ПРЕДШ[v]. При этом записи в списках смежностей состоят из грех компонент: поля имени узла, поля веса соответствующей дуги и поля ссылки на следующую запись.
Пусть р: v=v0,v1,...,vk=w — путь в сети G от узла v до узла w (v-w-путь); положим
c(p)=c(v0, v1)+...+c(vk-1, vk).
Число с(р) назовем длиной пути р. Наименьшую из длин v-w-путей назовем расстоянием от v до w, а тот v-w-путь, длина которого равна расстоянию от v до w, — кратчайшим v-w-путем. Ясно, что расстояние от v до w может отличаться от расстояния от w до V.
Задача о кратчайшем пути (ЗКП) между фиксированными узлами: в заданной сети G с двумя выделенными узлами s и t найти кратчайший s-t-путь.
Отметим сразу, что ЗКП можно рассматривать и в неориентированных взвешенных графах, заменив каждое ребро {v,w} графа двумя дугами (v,w) и (w,v) и считая, что c(v,w)=c(w,v)=c({v,w}).
Далее, если в невзвешенном графе положить вес каждого ребра равным единице, то получим данное ранее определение длины пути (см.гл.2 и гл.4) как числа ребер. С этой точки зрения рассмотренная в гл.4 задача построения кратчайшего по числу ребер пути есть частный случай сформулированной только что задачи.
В первом параграфе рассматривается ЗКП в произвольных сетях, во втором и третьем рассмотрены важные частные случаи этой задачи, четвертый и пятый параграфы посвящены разбору естественных модификаций ЗКП и, наконец, в шестом параграфе рассматривается ЗКП между всеми парами узлов заданной сети.
Можно дать много практических интерпретаций ЗКП. Одна из таких была дана в главе первой, где была рассмотрена задача нахождения самого короткого пути между городами. Другая, менее очевидная ситуация возникает в задаче выбора самого надежного пути передачи информации в некоторой информационной сети.
Пусть имеется информационная сеть, связывающая n пунктов связи, и для каждого канала (v,w) передачи информации от пункта связи v к пункту w известна вероятность P(v,w) его безаварийной работы. Предположим, что аварии каналов не зависят друг от друга. Тогда вероятность исправности пути q: s=v0,v1,...,vk=t передачи информации от s до t равна
P(q) = П{P(vi-1,v1) : i=l,2,...,k}.
Самым надежным путем передачи информации от s к t естественно считать тот путь q, для которого значение P(q) максимально.
Рассмотрим сеть G*. узлы которой соответствуют пунктам связи, а дуги — каналам передачи информации, и для дуги (v,w) полагаем c(v,w) = -logP(v,w). Пусть в этой сети для узлов s и t решена ЗКП, то есть найден кратчайший s-t-путь q: s=vo,v1,…,vk=t. Иначе говоря, c(q) = ∑{c(vi-1,v1):i=l,2,...,k}→min среди всех s-t-путей, то есть ∑{-logP(vi-1,v1):i=l,2,...,k}→min.
Тогда log(П{P(vi-1,v1):i=l,2,...,k})→max.Отсюда следует, что для кратчайшего s-t-пути q вероятность правильного прохождения сигнала максимальна среди всех s-t-путей. Таким образом, кратчайший s-t-путь в сети G* определяет самый надежный путь передачи информации в информационной сети.
Дата добавления: 2021-07-22; просмотров: 745;











