Цепи и пути в графах.
В этом разделе будем рассматривать только связные неориентированные графы. Нетрудно проверить, что и ПВГ-дерево, и ПВШ-дерево действительно являются деревьями, и более того — корневыми деревьями (см. гл.2), причем корнями этих деревьев являются те вершины, с которых начинался поиск (собственно поэтому они и в ПВГ и в ПВШ названы корневыми вершинами).
Ранее, в главе 2, мы условились считать, что если в ориентированном графе имеется дуга (v,w), то v — отец w, a w — сын v. Легко видеть, что даваемые алгоритмами 4.1 и 4.2 значения переменных ОТЕЦ[w] согласуются с ранее введенным понятием, а именно, если v=ОТЕЦ[w], то (v,w)  E.
E.
Напомним, что вершина v называется предком вершины w. и, соответственно, w — потомком v, если в корневом дереве существует путь от v до w. Например, в корневом дереве ПВШ(1) из рис.4.2 вершина 8 является потомком вершины 2. В следующей теореме формулируются полезные свойства ПВГ-деревьев.
Теорема 4.3.Пусть Т — ПВГ-дерево связного неориентированного графа G=(V,E), и пусть {u,w}  E. Тогда либо u — потомок w, либо w потомок u в корневом дереве Т.
E. Тогда либо u — потомок w, либо w потомок u в корневом дереве Т.
Предположим без ограничения общности, что вершина и будет просмотрена раньше, чем w. Рассмотрим процесс поиска в глубину, начиная с первого вызова процедуры ПВГ(u) (см. алгоритм 4.1.), и до первого вызова ПВГ(w). Это означает, что мы прошли по некоторым ребрам из вершины u в w. Но именно эти пройденные ребра мы и относим в ПВГ-дерево Т. Они образуют путь из u в w, следовательно, вершина u является предком вершины w в корневом дереве Т.
Понятно, что ПВШ-дерево не обладает свойством, сформулированным в теореме 4.3. Например, в ПВШ(1)-дереве, изображенном на рис.4.2, ни вершина 3 не является потомком вершины 6, ни вершина 6 не является потомком вершины 3 (говорят, что такие вершины несравнимы в корневом дереве).
Как в ПВГ-дереве, так и в ПВШ-дереве для каждой вершины w, существует единственный путь из корня v в w. Как построить этот путь? Это несложно делается с помощью массива ОТЕЦ. Отметим только, что под путем в орграфе мы договорились понимать в зависимости от степени удобства, либо последовательность ребер, либо последовательность вершин (см.гл.2). В предлагаемом ниже алгоритме 4.3 требуемый путь идентифицируется последовательностью вершин. Предполагается, что перед работой этого алгоритма работала либо процедура ПВГ(v), либо процедура ПВШ(v).
АЛГОРИТМ 4.3. ПОСТРОЕНИЕ ПУТИ
Данные: корневая вершина поиска v, вершина w. массив ОТЕЦ.
 Результат: СТЕК, содержащий последовательность вершин, образующих v-w-путь.
Результат: СТЕК, содержащий последовательность вершин, образующих v-w-путь.
Понятно, что последовательность вершин v=v0,v1,...,vk=w, полученная считыванием СТЕКА, образует как v-w-путь в корневом дереве Т (или D), так и v-w-цепь в исходном графе G.
Оказывается, что пути, построенные поиском в ширину, обладают очень полезным свойством, а именно, справедлива.
Теорема 4.4.Пусть D — ПВШ-дерево с корнем v связного неориентированного графа G=(V,E). Тогда для любой вершины w  V единственный v-w-путь в D определяет кратчайшую по числу ребер цепь среди всех v-w-цепей в графе G.
V единственный v-w-путь в D определяет кратчайшую по числу ребер цепь среди всех v-w-цепей в графе G.
Пусть кратчайшая по числу ребер v-w-цепь в графе G содержит t ребер. (Будем говорить, что вершина w находится на расстоянии t от v). Докажем теорему индукцией по расстоянию t.
Пусть t=l. Тогда всякая вершина u, находящаяся на расстоянии 1 от v, будет просмотрена из v, то есть для всех таких вершин u справедливо равенство ОТЕЦ[u]=v. Одновременно v — единственная вершина связного графа, для которой OTEЦ,[v]=nil. Значит, как это следует из алгоритма 4.3, поиск в ширину правильно определяет кратчайшие цепи до всех вершин, находящихся на расстоянии 1 от вершины v.
Пусть ПВШ-дерево правильно определяет кратчайшие цепи до всех вершин, находящихся на расстоянии t ≤ k от v.
Пусть вершина w находится на расстоянии k+1 от v и путь v=v0,v1...,vk+1=w — кратчайшая v-w-цепьв графе G. Ясно, что цепь v=v0,v1,...,vsявляется кратчайшей v-vs-цепью в графе G для всех s=l,...,k. В частности, вершина vkнаходится на расстоянии k от v.
Рассмотрим ПВШ(v)-дерево в тот момент, когда просматривается вершина w, и пусть u=OTEЦ[w]. В силу предположения индукции достаточно доказать, что и находится на расстоянии k от v. Если u=vk то теорема доказана. Пусть u≠vk. Так как ребро {vk,w}  E, и вершина w просмотрена из вершины u, то это означает, что вершина и просмотрена раньше чем vk. Следовательно, расстояние от v до и не больше, чем расстояние от v до vk, и, значит, вершина и находится на расстоянии не больше k от v. По предположению индукции алгоритм правильно определит кратчайшую цепь до u, и, следовательно, до w.
E, и вершина w просмотрена из вершины u, то это означает, что вершина и просмотрена раньше чем vk. Следовательно, расстояние от v до и не больше, чем расстояние от v до vk, и, значит, вершина и находится на расстоянии не больше k от v. По предположению индукции алгоритм правильно определит кратчайшую цепь до u, и, следовательно, до w.
Заметим, что пути, определяемые поиском в глубину, вообще говоря, не являются кратчайшими. Например, на рис.4.1 путь от вершины 1 до вершины 8 проходит через вершины 2,3,4,7,6 и имеет длину 6, а поиск в ширину (см.рис.4.2) определяет путь, проходящий через вершины 4,7, длиной 3.
Пути в лабиринте.
Под лабиринтам будем понимать множество точек на плоскости Р={(х,у) : 1≤х≤n, 1≤у≤m} с целочисленными координатами. Каждая точка р  Р находится в одном из двух состояний: «свободная» или «занятая». Даны две точки v,w
Р находится в одном из двух состояний: «свободная» или «занятая». Даны две точки v,w  Р ("вход» и «выход» из лабиринта). Требуется провести ломаную линию, соединяющую v и w, звенья которой параллельны осям координат и проходят через свободные вершины лабиринта Р.
Р ("вход» и «выход» из лабиринта). Требуется провести ломаную линию, соединяющую v и w, звенья которой параллельны осям координат и проходят через свободные вершины лабиринта Р.
Подобная задача является одной из центральных задач автоматического проектирования радиоэлектронных изделий, где в соответствии с заданной электрической схемой требуется осуществить соединения электрически связанных контактов схемы, будь то в кристалле (проектирование интегральных схем) или в монтажных слоях печатной платы (проектирование печатных плат). Справедливости ради, следует отметить, что при проектировании БИС или печатных плат речь идет о проведении соединений в нескольких слоях, иначе говоря, лабиринт имеет третье измерение — «толщину». Однако, разбор случая однослойного лабиринта, не отличаясь принципиально от случая многослойного лабиринта, проще для восприятия. Поэтому мы здесь рассмотрим только однослойный случай.
Для построения пути в лабиринте могут быть использованы как поиск в глубину, так и поиск в ширину. Действительно, достаточно по заданному лабиринту Р построить граф G=(V,E), в котором каждой свободной точке р  Р соответствует вершина p
Р соответствует вершина p  V, и две вершины p,q
V, и две вершины p,q  V считаются смежными, если их соответствующие точки p,q
V считаются смежными, если их соответствующие точки p,q  P являются соседними по горизонтали или вертикали. После построения графа остается применить один из алгоритмов поиска для построения пути в графе G между выбранными вершинами.
P являются соседними по горизонтали или вертикали. После построения графа остается применить один из алгоритмов поиска для построения пути в графе G между выбранными вершинами.
Однако, строить в явном виде граф G в общем-то бессмысленно. Можно сразу использовать один из алгоритмов поиска, применяя его к лабиринту, держа граф G в «уме». Рассмотрим, например, построение пути в лабиринте с использованием поиска в глубину.
Будем использовать четыре вспомогательных вектора d1,...,d4, где d1 = (1.0), d2 = (0,1), d3, = (-1,0). d4 =(0,-1).
Вектор dk служит для перехода от некоторой точки р из лабиринта к новой точке p+dk. Будем говорить, что вектор dk определяет k-ое направление. Фактически эти четыре вектора играют роль списков смежностей при задании графов, ибо служат для определения соседей каждой точки р  Р. Естественно (см. процедуру ПВГ1(v)), нам понадобится аналог переменной УКАЗ. Назовем переменную, которая будет указывать на первое непросмотренное из точки р
Р. Естественно (см. процедуру ПВГ1(v)), нам понадобится аналог переменной УКАЗ. Назовем переменную, которая будет указывать на первое непросмотренное из точки р  Р направление СТРЕЛКА[р].
Р направление СТРЕЛКА[р].
Случай СТРЕЛКА[р]=1 означает, что из точки р ни одно направление не просмотрено, если СТРЕЛКА[р] = k, где k≤4, то все направления с номером i для i<k из р уже просмотрены, то есть просмотрены точки p+di. Такая организация данных равносильна тому, что у каждой точки лабиринта р первой смежной вершиной считается p+d1, второй — p+d2 и т.д.
Лабиринт Р удобно задавать двумерным массивом P[l..n,l..m], состоящим из нулей и единиц, где нуль соответствует свободной точке лабиринта, а единица — занятой. Удобно считать, что P[l,i]=P[n,j]=P[k,l]=P[l,m]=l для всех 1≤ i,j ≤m, 1≤ k,l ≤n, то есть считать, что массив Р окаймлен единицами. Просмотренные по ходу поиска точки лабиринта, то есть нули массива Р, будем отмечать прямо в Р числом 2.
Кроме того, удобно использовать векторную запись, то есть вместо координатной записи точки лабиринта (v1,v2), использовать один символ v, где v= (V1,V2).
АЛГОРИТМ 4.4. ПУТЬ В ЛАБИРИНТЕ.
Данные: лабиринт Р, заданный массивом P[l..n,l..m]; векторы d1,...,d4, точки v — вход и w — выход из лабиринта.
 Результат: СТЕК, содержащий v-w-путь, если СТЕК=Ø, то v-w- пути в лабиринте Р не существует.
Результат: СТЕК, содержащий v-w-путь, если СТЕК=Ø, то v-w- пути в лабиринте Р не существует.
Отметим, что поскольку исходный массив окаймлен запрета ми (то есть первая и последняя строки и первый и последний столбцы заполнены единицами), в алгоритме нет нужды при просмотре каждой новой точки проверять, выходит или нет эта точка за границы лабиринта.
Теорема 4.5. Алгоритм 4.4 имеет сложность 0(n т).
Действительно, в худшем случае в процессе поиска в глубину придется просмотреть все точки лабиринта Р, прежде чем либо будет найден требуемый путь, либо можно будет утверждать, что искомого пути не существует. В лабиринте содержится n∙m точек, а количество операций, необходимых для обработки каждой точки, ограничено сверху константой. Из этих двух фактов вытекает, что алгоритм 4.4 имеет вычислительную сложность О(n∙m), что завершает доказательство.
На рис.4.3 приведен пример работы алгоритма 4.4 ПУТЬ В ЛАБИРИНТЕ. Здесь знаком * отмечены точки входа в лабиринт Р и выхода из лабиринта с координатами (2,6) и (7.5) соответственно. Отметим, что в нашей постановке задачи вход и выход из лабиринта могут располагаться в любом месте лабиринта, а не только на его границе, как это обычно предполагается.

| |||||||||||||||||||||||||||||||||
| * | * | ||||||||||||||||||||||||||||||||
| * | * | ||||||||||||||||||||||||||||||||




В следующей таблице показано, как менялся СТЕК в ходе работы алгоритма 4.4 для лабиринта, изображенного на рис.4.3. Числа в левой колонке означают очередной такт работы цикла в строках 2-12 алгоритма 4.4. (Содержание СТЕКа дано после очередного прохода цикла 2-12). Отметим, что после попадания в тупиковую точку (6,6), происходит возврат через точку (5,6) в точку (4,6), из которой возобновляется поиск в другом направлении.
| СТЕК | |
| (2,6); (3,6) | |
| (2.6); (3,6); (4,6) | |
| (2,6); (3,6); (4,6); (5,6) | |
| (2,6); (3,6); (4,6); (5,6); (6,6) | |
| (2,6); (3,6); (4,6); (5,6) | |
| (2,6); (3,6); (4,6) | |
| (2,6); (3,6); (4,5) | |
| … | … |
| (2,6);(3,6);(4,6);(4,5);(4,4);(4,3);(5,3);(6,3);(7,3); (8,3);(8,4);(8,5);(7,5) |
Рассмотрим теперь более сложную задачу — задачу построения пути в лабиринте с минимальным числом изгибов. Иначе говоря, ломаная, соединяющая две заданные точки, должна иметь наименьшее число звеньев среди всех ломаных, которые также соединяют заданные точки. Например, на рис.4.4 путь, соединяющий точки (2,6) и (7,5) имеет 4 изгиба — (4,6), (4.3), (8,3) и (8,5). В то же время путь, проходящий через точки (2.3). (8,3), и имеющий только их в качестве изгибов, имеет таких точек только 3.
Задача проведения пути с минимальным числом изгибов есть также одна из задач автоматического проектирования БИС и печатных плат, поскольку такие проводники более технологичны в производстве.
Для решения этой задачи мы используем поиск в ширину, примененный непосредственно к лабиринту. Вот основные идеи этого алгоритма.
Поиск начинаем с точки входа v и считаем, что эта точка образует нулевой фронт распространения волны. Все точки лабиринта, до которых можно построить путь из v без поворотов (то есть двигаясь по какой-либо прямой) объявляем точками первого фронта, и для каждой такой точки запоминаем направление, по которому мы в нее пришли.
В общем случае, когда построен очередной k-ый фронт волны. (k+1)-ый фронт строится следующим образом. Отнесем в него все точки лабиринта, до которых можно дойти от какой-либо точки k-го фронта, двигаясь по какой-нибудь прямой. Здесь необходимо иметь в виду, что одна и та же точка может быть достигнута из разных точек k-го фронта по разным направлениям, поэтому массив ОТЕЦ, определенный ранее в алгоритме 4.2, здесь неприменим. Будем для точек (k+1)-го фронта хранить все направления, по которым они могут быть достигнуты из k-го фронта.
Распространение волны завершаем либо в тот момент, когда мы достигнем точки выхода w, либо когда ни одной новой точки нельзя достигнуть. В первом случае искомый путь существует и может быть построен с помощью расставленных ранее меток, отвечающих за направление прихода в точку; во втором случае ни одного пути от входа v до выхода w не существует.
Перейдем к формальному описанию алгоритма. Будем использовать две очереди. В ОЧЕРЕДЬ1 будем хранить последний построенный фронт распространения волны, в ОЧЕРЕДЬ2 будем сбрасывать все точки нового, строящегося фронта. С помощью всего лишь одного числа Р[u], где u — точка лабиринта Р, можно хранить информацию как о номере фронта, в который попадает точка u, так и о всех направлениях, по которым она достигнута из предыдущего фронта.
Пусть свободная точка лабиринта и попадает в k-ый фронт распространения волны. Положим
Р[u]=20∙(k+1) + а120 + а221 + a322 + а423,
где коэффициент аi, равен 1, если точка и помечена по i-му направлению, заданному вектором di, и аi, = 0 в противном случае. Зная число Р[u], номер фронта к вычисляется просто: k+1 = 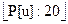 , или в соответствии с синтаксисом Паскаля:
, или в соответствии с синтаксисом Паскаля:
k+1 = P[u] div 20.
Для того, чтобы определить, по каким направлениям пришли в точку и нужно число P[u] mod 20 (остаток от деления Р[u] на 20) разложить по степеням двойки. Если в разложении присутствует число 2i, то это означает, что мы приходили в эту точку по (i+1 )-му направлению (и, быть может, по другим тоже).
Ниже массив P[1..n,l..m] и векторы di, (i=l,2,3,4) те же самые, что и ранее при построении пути в лабиринте. Вначале опишем процедуру, вычисляющую значения Р[u]. Как и ранее, v — вход, a w — выход из лабиринта Р.
На рис.4.4 приведен пример работы процедуры ПОМЕЧИВАНИЕ. Обозначения на этом рисунке те же, что и на рис.4.3. Точка входа имеет координаты (2,3), выхода —(5,5).
Обращаем внимание читателя на то, что при построении второго фронта точка (4,5) помечена из двух разных точек, сначала по четвертому направлению из точки (4,3), затем — по первому из точки (2,5).
| * |  * *
| |||||||||||||||||||||||
| * | * | |||||||||||||||||||||||




Как по размеченному полю восстановить требуемый путь? Также как и в алгоритме 4.3 ПОСТРОЕНИЕ ПУТИ путь строится «обратным ходом». Мы начинаем построение пути с конечной точки w. Для этого число P[w] mod 20 раскладываем по степеням двойки и фиксируем какое-нибудь число i такое, что
2i-1 присутствует в этом разложении. Это означает, что точка w помечена по i-му направлению.
Двигаемся теперь из w по направлению, противоположному i-му, до тех пор, пока не встретим точку и такую, что двоичное разложение числа P[u] mod 20 не содержит 2i-1. Это означает, что точка и помечена по другому направлению. Выбираем теперь какое-нибудь новое значение i, для которого 2i-1 входит в разложение числа P[u] mod 20, и продолжаем процесс из точки u.
Алгоритм завершает работу в момент, когда P[u] mod 20 = 0, ибо единственной точкой, удовлетворяющей этому условию, является точка входа — v.
Теперь мы можем формально описать весь алгоритм построения пути в лабиринте с минимальным числом изгибов. Без формального описания будем использовать функцию РАЗЛОЖЕHИE(i,x), значение которой — true, если число 2i-1 входит в разложение целого числа х по степеням двойки, и false в противном случае, а также функцию ВЫБОР(х), значением которой является число i такое, что 2i-1 входит в разложение числа х по степеням двойки. Если таких чисел несколько, то выбирается любая из них.
АЛГОРИТМ 4.5. МИНИМАЛЬНЫЙ ПО ЧИСЛУ ИЗГИБОВ ПУТЬ В ЛАБИРИНТЕ.
Данные: лабиринт Р, заданный массивом P[l..n,l..m]; векторы d1,…,d4, точки v —вход и w — выход из лабиринта.
 Результат: СТЕК, содержащий v-w-путь с минимальным числом изгибов, или сообщение, что такого пути не существует.
Результат: СТЕК, содержащий v-w-путь с минимальным числом изгибов, или сообщение, что такого пути не существует.
В приведенном алгоритме в строке 7 происходит поиск одного из тех направлений, по которым была достигнута точка u. Отметим, что такой анализ проводится не всегда, а только в тех тючках, на которых закончилось предыдущее направление, ибо далее в цикле 9-12 происходит движение по имеющемуся направлению, до тех пор пока это возможно.
Приведенная формализация алгоритма построения пути с наименьшим числом изгибов не является единственно возможной. Несложно реализовать алгоритм так, чтобы при разметке лабиринта, учитывать только номер фронта. В этом случае реализация процедуры ПОМЕЧИВАНИЕ будет проще, но при построении пути придется достаточно долго искать направление, которое показывает наточку предыдущего фронта.
Легко видеть, что справедлива следующая
Теорема 4.6.Алгоритм 4.5 имеет сложность O(nm).
ЗАДАЧИ
1. Написать алгоритм поиска в глубину для графа, заданного а) матрицей смежности, б) массивом смежностей.
2. Написать алгоритм поиска в ширину для графа, заданною а) матрицей смежности, б) массивом смежностей.
3. Модифицировать алгоритмы 4.1 и 4.2 так, чтобы на выходе были получены связные компоненты неориентированного графа, представленные списками вершин.
4. Написать алгоритм, проверяющий ацикличность данного графа, а) модифицируя алгоритм 4.1, б) модифицируя алгоритм 4.2.
5. Граф G=(V,E) называется двудольным, если существует разбиение V=V1  V2, V1
V2, V1  V2=Ø такое, что каждое ребро е={а,b} имеет вид a
V2=Ø такое, что каждое ребро е={а,b} имеет вид a  V1, b
V1, b  V2 Предложить два алгоритма, проверяющих, будет ли данный граф двудольным, за время 0(n+m): один, основанный на поиске в глубину, другой — на поиске в ширину.
V2 Предложить два алгоритма, проверяющих, будет ли данный граф двудольным, за время 0(n+m): один, основанный на поиске в глубину, другой — на поиске в ширину.
6. Написать алгоритм построения пути в лабиринте, основанный на поиске в ширину. Каким свойством будет обладать построенный этим методом путь?
7. Представить детальную реализацию функций РАЗЛОЖЕНИЕ(k,х) и ВЫБОР(х), использованных в алгоритме 4.5.
8. Модифицировать алгоритм 4.5 так, чтобы СТЕК содержал кроме точек входа и выхода только все точки изгибов пути.
9. Применить процедуру ПОМЕЧИВАНИЕ(v,w) к полю, изображенному на рис.4.2, меняя местами вход и выход, то есть v=(5,5), w=(2,3).
10. На шахматной доске стоят черная пешка и белый конь. Напишите два алгоритма, определяющих маршрут белого коня, завершающийся уничтожением черной пешки.
Глава V
Дата добавления: 2021-07-22; просмотров: 621;











