Случай неотрицательных весов. Алгоритм Дейкстры.
Описываемый в этом разделе алгоритм позволяет вычислять в сети с неотрицательными весами расстояния от фиксированного узла s до всех остальных узлов более эффективно, чем алгоритм Форда-Беллм!анк. Этот алгоритм был предложен в 1959 году Дейкстрой.
В основе алгоритма Дейкстры лежит принцип «жадности», заключающийся в последовательном вычислении расстояний сначала до ближайшего к s узла, затем до следующего ближайшего и т.д. Для удобства изложения обозначим через d(v) расстояние от s до v, то есть длину кратчайшего s-v-пути в сети G.
Первый ближайший к узлу s узел v вычисляется просто: это сам узел s, находящийся на нулевом расстоянии от s, то есть d(s)=0.
Пусть ближайшие к узлов к узлу s определены, и для всех них вычислены расстояния d(v), то есть определено множество S={v1=s, v2,..., vk},причем выполняются неравенства:
(1) 0 = d(v1) ≤ d(v2) ≤ ... ≤d(vk);
(2) d(vk) ≤ d(v), для всех v 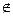 V.
V.
Здесь следует иметь ввиду, что последнее неравенство имеет «потенциальный» характер, а именно, мы считаем известными значения расстояний только для узлов v1, v2,..., vk, а для всех остальных узлов расстояния еще не вычислены, но для них известно, что неравенства (2) будут выполняться.
Найдем следующий ближайший к s узел сети G. Для каждого w 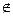 S положим
S положим
D(w)=min{d(v)+c(v,w) : v  S}, (6.3)
S}, (6.3)
Можно отметить, что тогда D(w) определяет стоимость минимального s-w-пути среди всех s-w-путей, все узлы в котором, кроме w, принадлежат S.
Выберем теперь узел w* 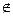 S под условием:
S под условием:
D(w*)=min{D(w): w 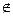 S}. (6.4)
S}. (6.4)
Оказывается, что узел w* является самым близким к s среди всех узлов, не входящих в S, и, более того, расстояние от узла s до узла w* равно D(w*), то есть справедливо равенство d(w*)=D(w*).
Обоснуем вначале равенство d(w*)=D(w*). Пусть p:s=w0,w1,...,wr=w* — произвольный s-w*-nyrb в сети G. Достаточно доказать неравенство D(w*) ≤ с(р). Среди всех узлов пути р выберем узел w с наименьшим номером среди тех, которые не входят в множество S. Так как начальный узел пути р входит в S, а конечный — не входит в S, то такой номер j найдется. Итак wj-1  S, wj
S, wj 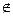 S. Тогда из условия (6.3) и определения стоимости пути вытекают неравенства
S. Тогда из условия (6.3) и определения стоимости пути вытекают неравенства
D(wj) ≤ d(wj-1) + c(wj-1, wj) ≤ c(w0, w1) +...+ c(wj-1, wj) = c(q),
где через q обозначен подпуть пути р от s до w,.
Но из условия неотрицательности весов дуг следует, что c(q) ≤c(p), кроме того, из условия (6.4) следует, что D(w*)≤D(wj). С учетом этих неравенств получаем, что D(w*)≤c(p). Отсюда следует, что d(w*)=D(w*).
Осталось убедиться, что узел w является (k+1)-ым ближайшим к s узлом. Для этого достаточно доказать неравенство d(w*)≤d(w) для всех w 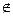 S. Зафиксируем s-w*-путьр* и s-w-путь р, для которых c(p*)=d(w) и c(p)=d(w). В силу доказанного только что равенства D(w*)=d(w*) можно считать, что в пути р* все узлы, кроме w*, лежат в S. Тогда в силу условия (6.4) D(w*) ≤ D(w), и, повторяя вышеприведенные рассуждения, приходим к неравенству D(w) ≤ с(р). Отсюда c(p*)=d(w*)=D(w*)≤c(p)=d(w), что и требовалось доказать.
S. Зафиксируем s-w*-путьр* и s-w-путь р, для которых c(p*)=d(w) и c(p)=d(w). В силу доказанного только что равенства D(w*)=d(w*) можно считать, что в пути р* все узлы, кроме w*, лежат в S. Тогда в силу условия (6.4) D(w*) ≤ D(w), и, повторяя вышеприведенные рассуждения, приходим к неравенству D(w) ≤ с(р). Отсюда c(p*)=d(w*)=D(w*)≤c(p)=d(w), что и требовалось доказать.
Итак, выбирая узел w  V\S под условием (6.4) и добавляя найденный узел к S, мы расширяем множество узлов, до которых вычислено расстояние, на один элемент. Следовательно, повторяя процесс расширения множества S п-1 раз, мы вычислим расстояния до всех узлов сети G.
V\S под условием (6.4) и добавляя найденный узел к S, мы расширяем множество узлов, до которых вычислено расстояние, на один элемент. Следовательно, повторяя процесс расширения множества S п-1 раз, мы вычислим расстояния до всех узлов сети G.
При формальной записи алгоритма Дейкстры (алгоритм 6.3) ход вычислений расстояний от s до остальных узлов v будем отражать в массиве с именем D. По окончании работы алгоритма будем иметь равенства D[v]=d(v) для всех v  V. Вместо множества S удобнее оперировать с дополнением S до V, которое мы обозначим F. Без формального описания используется функция MIN(F), значением которой является такой узел w
V. Вместо множества S удобнее оперировать с дополнением S до V, которое мы обозначим F. Без формального описания используется функция MIN(F), значением которой является такой узел w  F, что справедливо равенство D[w]=min{D[v] : v
F, что справедливо равенство D[w]=min{D[v] : v  F}, иначе говоря, это тот самый элемент, который следует добавить к S, или, что то же самое, удалить из F.
F}, иначе говоря, это тот самый элемент, который следует добавить к S, или, что то же самое, удалить из F.
АЛГОРИТМ 6.3. ДЕЙКСТРА
(* нахождение расстояний от фиксированного узла до всех остальных в сети с неотрицательными весами *)
Данные: Сеть G=(V,E,c), заданная матрицей весов А[1..n, 1..n]; выделенный узел s.
Результаты: Расстояния D[v] от s до всех узлов v  V.
V.
Для доказательства корректности алгоритма 6.3 заметим, что при входе в очередную k-ую итерацию цикла 5-11 уже определены к ближайших к s узлов и вычислены расстояния от s до каждого из них. При этом первоначальные значения расстояний вычислены в строке 4. Как показано выше, выполнение строки 7 правильно определяет (k+1)-ый ближайший к s узел. Удаление w из F влечет, что D[w] больше меняться не будет, но по доказанному ранее D[w]=d(w). Осталось заметить, что выполнение строки 10 в каждой итерации цикла 5-11 позволяет правильно вычислять значения D[v], Следовательно, алгоритм 6.3 правильно вычисляет расстояния от фиксированного узла до всех остальных узлов сети.
Теорема6.2. Алгоритм Дейкстры имеет сложность O(n2).
Пусть найдены расстояния до k ближайших к s углов. Определение расстояния до (k+l)-гo узла требует в строке 7 числа операций пропорционального (n-k). Пересчет D[v] в строке 10 требует числа операций пропорционального (n-k). Окончательно, общее число операций в алгоритме Дейкстры пропорционально n+(n-l)+...+l=n(n-l)/2, то есть равно O(n2).

| K | S=V\F | D[1] | D[2] | D[3] | D[4] | D[5] | D[6] |
| {1=s} | ∞ | ∞ | |||||
| {1;4} | ∞ | ||||||
| {1;4;2} | |||||||
| {1;4;2;6} | |||||||
| {1;4;2;6;3} | |||||||
| {1;4;2;6;3;5} |
Рис.6.2. Работа алгоритма Дейкстры.
Вычислив расстояния от s до всех остальных узлов v, построение самих кратчайших s-v-путей можно вести по алгоритму 6.2.
Можно дать и другую, графическую интерпретацию работы алгоритма Дейкстры. Введем для этого массив ОТЕЦ и строку 10 алгоритма Дейкстры заменим аналогично тому, как была заменена строка 6 в алгоритме Форда-Беллмана, на строки 6.1, 6.2, 6.3. Будем каждый раз при вычислении расстояния до (k+1 )-го ближайшего узла w относить дугу (OTEЦ,[w], w) в дерево К Дерево К назовем деревом кратчайших путей. Ясно, что структура дерева К будет такой: К — это корневое дерево с корнем в s, и для всякой вершины v  V единственный в К s-v-путь будет кратчайшим s-v-путем в сети G.
V единственный в К s-v-путь будет кратчайшим s-v-путем в сети G.
Для сети, изображенной ранее на рис. 6.2, ход построения дерева кратчайших путей показан ниже на рис. 6.3.

Рис 6.3. Процесс построения дерева кратчайших путей
Уже неоднократно отмечалось, что редкие сети (m«n2) удобнее представлять списками или массивом смежностей. Будем
считать далее, что граф представлен списками смежностей СЛЕДМ.
Обратим внимание на то, что в алгоритме Дейкстры многократно, (а именно, при каждом входе в цикл 5-11) приходится находить минимальный элемент массива D[v], Между тем, в главе 3. где рассматривалась задача сортировки данных, была введена структура данных, позволяющая эффективно определять максимальный элемент — сортирующее дерево массива.
Применим эту технику здесь, с той лишь разницей, что в корне сортирующего дерева будет находиться минимальный, а не максимальный, как в главе 3, элемент массива. Для этого в алгоритме построения сортирующего дерева, а значит и в процедуре ПЕРЕСЫПКА, достаточно сменить все знаки неравенств на противоположные. Иначе говоря, мы считаем, что если D[v] элемент в сыне того узла, где находится D[w], то D[v]<D[w].
Необходимо только позаботиться о том, чтобы при каждом изменении D[v] новое значение D[v] не нарушало структуры сортирующего дерева, что и осуществляется в строках 16-19 предложенного ниже алгоритма.
АЛГОРИТМ 6.4
(* алгоритм Дейкстры для редких сетей *)
Данные: Сеть G=(V,E,c), заданная списками смежностей СЛЕД[у]; выделенный узел s.
 Результаты: Расстояния D[v] от s до всех остальных вершин ve V.
Результаты: Расстояния D[v] от s до всех остальных вершин ve V.
Теорема 6.3.Алгоритм 6.4 имеет сложность O(mlogn).
В строке 4 осуществляется построение сортирующего дерева для массива из (n-l)-гo элемента. Сложность такого построения есть О(n) (теорема 3.3). При каждом входе в цикл 5-19 корень дерева удаляется, и осуществляется процедура ПЕРЕСЫПКА для восстановления структуры данных. Поскольку глубина дерева В есть 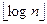 , то сложность выполнения один раз процедуры ПЕРЕСЫПКА есть O(logn). Следовательно, суммарная сложность удаления корня из дерева есть O(nlogn). Легко видеть, что выполнение цикла 11-18 приводит к тому, что каждая дуга сети анализируется ровно один раз, причем каждый раз при рассмотрении дуги возможен вызов процедуры ПЕРЕСЫПКА для передвижения нового значения D[v] по дереву В. Поэтому суммарная сложность выполнения цикла 1 1-18 есть O(mlogn). Окончательно имеем
, то сложность выполнения один раз процедуры ПЕРЕСЫПКА есть O(logn). Следовательно, суммарная сложность удаления корня из дерева есть O(nlogn). Легко видеть, что выполнение цикла 11-18 приводит к тому, что каждая дуга сети анализируется ровно один раз, причем каждый раз при рассмотрении дуги возможен вызов процедуры ПЕРЕСЫПКА для передвижения нового значения D[v] по дереву В. Поэтому суммарная сложность выполнения цикла 1 1-18 есть O(mlogn). Окончательно имеем
O(n)+O(nlogn)+O(mlogn)=O(mlogn),
ибо остается в силе предположение о том, что m≥n.
Дата добавления: 2021-07-22; просмотров: 551;











