Задача о максимальном пути и сетевые графики.
Задача о максимальном пути формулируется следующим образом: в заданной сети G=(V,E,c) с выделенным узлом s, для каждого узла v  V найти s-v-путь, имеющий максимальную длину среди всех возможных s-v-путей в сети G.
V найти s-v-путь, имеющий максимальную длину среди всех возможных s-v-путей в сети G.
Отметим, что имеет смысл решать эту задачу лишь в сетях, не содержащих контуров положительной длины. Рассмотрев тогда сеть, отличающуюся от исходной только изменением знаков весов дуг, получим сеть, в которой нет контуров отрицательной длины. Применяя к новой сети алгоритм Форда-Беллмана, можно построить кратчайшие s-v-пути, которые будут путями максимальной длины в исходной сети.
Впрочем, задачу о максимальном пути в общем случае можно решать и непосредственно, заменяя в алгоритме Форда-Беллмана строку 6 на строку
6' forw  V doD[v] := max(D[v], D[w]+A[w,v]);
V doD[v] := max(D[v], D[w]+A[w,v]);
Разумеется, решая таким образом задачу о максимальном пути, вес несуществующих дуг следует положить равным -∞.
Важный частный случай сети с неотрицательными весами дуг в предположении отсутствия контуров положительной длины сводится к случаю отсутствия контуров в сети. Следовательно, задача о максимальном пути в частном случае может быть решена алгоритмом 6.6, в котором +∞ заменяется на
-∞ (строка 3), а min на шах (строка 6). Несложное доказательство корректности исправленного таким образом алгоритма 6.6 мы предоставляем читателю.
Отметим, что замена всех минимумов в алгоритме Дейкстры (строки 7 и 10) на максимумы не позволяет получить алгоритм решения задачи о максимальном пути. Для примера достаточно рассмотреть сеть, изображенную на рис.6.5. Здесь модификация алгоритма Дейкстры, при которой все минимумы заменены на максимумы неправильно определит путь максимальной длины от узла s до узла 2.
 Итак, алгоритм Форда-Беллмана и алгоритм 6.6 легко могут быть модифицированы для вычисления длин максимальных
Итак, алгоритм Форда-Беллмана и алгоритм 6.6 легко могут быть модифицированы для вычисления длин максимальных
s-v- *1 путей. Сами же пути с помощью вычисленных Задача о максимальном пути в бесконтурной сети имеет большое практическое значение. Она является важнейшим звеном в методах сетевого планирования работ по осуществлению некоторого проекта.
Многие крупные проекты, такие как строительство дома, изготовление станка, разработка автоматизированной системы бухгалтерского учета и т.д., можно разбить на большое количество различных операций (работ). Некоторые из этих операций могут выполняться одновременно, другие — только последовательно: одна операция после окончания другой. Например, при строительстве дома можно совместить во времени внутренние отделочные работы и работы по благоустройству территории, однако возводить стены можно только после того, как будет готов фундамент.
Задачи планирования работ по осуществлению некоторого проекта состоят в определении времени возможного окончания как всего проекта в целом, так и отдельных работ, образующих проект; в определении резервов времени для выполнения отдельных работ; в определении критических работ, то есть таких работ, задержка в выполнении которых ведет к задержке выполнения всего проекта в целом; в управлении ресурсами, если таковые имеются и т.п.
Здесь мы разберем основные моменты одного из методов сетевого планирования, называемого методом критического пути (МКП).
Метод был разработан в конце пятидесятых годов Дюпоном и Ремингтоном Рандом для управления работой химических заводов фирмы "Дюпон де Немур" (США).
Пусть некоторый проект W состоит из работ v1...,vn. для каждой работы vk известно, или может быть достаточно точно оценено время ее выполнения t(vk). Кроме того, для каждой работы vk известен, возможно пустой, список ПРЕДШ(vк) работ, непосредственно предшествующих выполнению работы vk. Иначе говоря, работа vk может начать выполняться только после завершения всех работ, входящих в список ПРЕДШ(vк).
Для удобства, в список работ проекта W добавим две фиктивные работы s и t, где работа s обозначает начало всего проекта W, а работа t — завершение работ по проекту W. При этом будем считать, что работа s предшествует всем тем работам v  W, для которых список ПРЕДШ(v) пуст, иначе говоря, для всех таких работ v
W, для которых список ПРЕДШ(v) пуст, иначе говоря, для всех таких работ v  W положим ПРЕДШ(v)={s}. Положим далее ПРЕДШ(s) = Ø, ПРЕДШ(t)={v
W положим ПРЕДШ(v)={s}. Положим далее ПРЕДШ(s) = Ø, ПРЕДШ(t)={v  W : v не входит ни в один список ПРЕДШ(w)}, то есть считаем, что работе t предшествуют все те работы, которые могут выполняться самыми последними. Время выполнения работ s и t естественно положить равными нулю; t(s)=t(t)=0.
W : v не входит ни в один список ПРЕДШ(w)}, то есть считаем, что работе t предшествуют все те работы, которые могут выполняться самыми последними. Время выполнения работ s и t естественно положить равными нулю; t(s)=t(t)=0.
Весь проект W теперь удобно представить в виде сети G=(V,E,c), где сеть G=(V,E,c) определим по правилам:
1. V=W, то есть множеством узлов объявим множество работ;
2. E={(v,w) : v  ПРЕДШ(w)}, то есть отношение предшествования задает дуги в сети;
ПРЕДШ(w)}, то есть отношение предшествования задает дуги в сети;
3. c(v,w)=t(w).
Так построенную сеть G часто называют сетевым графиком выполнения работ по проекту W. Легко видеть, что списки смежностей этой сети ПРЕДШ[v] совпадают с заданными для проекта списками предшествующих работ ПРЕДШ(v).
Понятно, что сетевой график любого проекта не может содержать контуров. Действительно, пусть узлы vkl,vk2,...,vkr=vk1 образуют контур в сети G. Это означает, что работа vk2 не может начаться раньше, чем будет завершена работа vk1 работа vk3 — раньше, чем завершится работа vk2, и т.д., и, наконец, vkr = vk| -— раньше, чем будет завершена работа vkr-1. Но тогда никакая из работ vk1...,vkr никогда не сможет быть выполнена. А каждый реальный проект должен допускать возможность его завершения. Следовательно, в сетевом графике нет контуров.
Отсутствие контуров в сети G позволяет пронумеровать работы проекта W таким образом, чтобы для каждой дуги (vi, vj) сети G выполнялось условие i<j (лемма 6.3). Напомним, что осуществить такую нумерацию узлов сети G можно с помощью алгоритма 6.5 ТОПСОРТ. Поэтому в дальнейшем будем считать, что узлы в сети G топологически отсортированы.
| n | Наименование работы | Предшествующие работы | Время выполнения |
| Закладка фундамента | Нет | ||
| Возведение коробки задания | |||
| Монтаж электропроводки | |||
| Сантехмонтаж | |||
| Настил крыши | |||
| Отделочные работы | 3,4 | ||
| Благоустройство территории |
 Рис 6.6 Проект строительства дома и его сетевой график
Рис 6.6 Проект строительства дома и его сетевой график
Конечной целью построения сетевой модели является получение информации о возможных сроках выполнения как отдельных работ, так и о возможном сроке выполнения всего проекта в целом.
Обозначим через РВЫП(v) (соответственно PHAЧ(v)) наиболее ранний возможный срок выполнения работы v (соответственно наиболее ранний возможный срок начала работы v). Удобно считать, что РВЫП(s)=PHAЧ(s)=0. Поскольку начать выполнять работу v можно только после того, как будут выполнены все работы, предшествующие данной работе v, то получим следующие формулы для расчета значений PHAЧ(v) и РВЫП(v):
PHAЧ(v) = max{ РВЫП(w): w  ПРЕДШ(v)},
ПРЕДШ(v)},
РВЫП(v) = PHAЧ(v) + t(v).
Легко видеть, что значение РВЫП(v) равно длине максимального s-v-пути в сети G. Поэтому, для вычисления значений РВЫП(v) можно использовать алгоритм 6.6 вычисления длин минимальных путей в бесконтурной сети, в котором все минимумы заменены на максимумы. При этом значение РВЫП(t) дает наиболее ранний возможный срок завершения всего проекта в целом.
Ради полноты приведем здесь формальную запись алгоритма, непосредственно вычисляющего характеристики РНАЧ и РВЫП.
АЛГОРИТМ 6.7.
(* расчет наиболее ранних возможных сроков начала и выполнения работ *)
Данные: Сетевой график G работ V, заданный списками ПРЕДШ(v), v  V.
V.
Результаты: Наиболее ранние возможные сроки начала и выполнения работ PHAЧ[v], РВЫП[v], v  V.
V.
Здесь, в алгоритме 6.7, узлы сетевого графика s и t обозначены соответственно через v0 и vn+1.
Значения РВЫП(v) и PHAЧ(v) для сетевого графика, изображенного ранее на рис.6.6, приведены на рис. 6.7. Из найденных значений следует, что этот проект не может быть завершен ранее чем через 20 единиц времени.
Пусть Т — плановый срок выполнения проекта W. Ясно, что Т должно удовлетворять неравенству Т ≥ PBЫП(vn+1).
Через ПВЫП(v) (соответственно ПНАЧ(у)) обозначим наиболее поздний допустимый срок выполнения (начала) работы v, то есть такой срок, который не увеличивает срок Т реализации всего проекта. Например, для работы 3 сетевого графика из рис. 6.6 имеем РНАЧ(3)=12, РВЫП(3)=14, но ясно, что начать работу 3 можно на единицу времени позже, поскольку это не повлияет на срок выполнения всего проекта, а вот задержка в реализации этой же работы на 2 единицы приведет к увеличению срока выполнения всего проекта на 1 единицу времени.
АЛГОРИТМ 6.8.
(* Расчет наиболее поздних сроков начала и окончания работ *) Данные: Сетевой график G работ V, заданный списками ПРЕДШ[v], v  V, плановый срок окончания проекта — Т. Результаты: Наиболее поздние допустимые сроки выполнения и начала работ ПВЫП[v] и ПНАЧ[v].
V, плановый срок окончания проекта — Т. Результаты: Наиболее поздние допустимые сроки выполнения и начала работ ПВЫП[v] и ПНАЧ[v].
Прямо из определений получаем справедливость равенств ПНАЧ(vn+1)=ПВЫП(vn+1)=Т. Поскольку произвольная работа v должна быть завершена до начала всех наиболее поздних допустимых сроков тех работ w, которым предшествует работа v, то получаем следующие формулы:
ПВЫП(v)=min{ПНАЧ(w): по всем w таким, что ПРЕДШ(w) 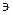 v},
v},
ПНАЧ(v)=ПВЫП(v)-t(v).
Вычислять значения ПВЫП(v) и ПНАЧ(v) можно, двигаясь по узлам сети G от vn+1 к v0. Все детали вычисления названных характеристик приведены выше в алгоритме 6.8.
Найденные значения возможных и допустимых сроков выполнения работ позволяют определить резервы времени для выполнения той или иной работы. В сетевом планировании рассматривают несколько различных и по-своему важных видов резерва работ. Мы здесь ограничимся лишь полным резервом (иногда его называют суммарным) времени выполнения работ. Он определяется по формуле:
PE3EPB(v)=ПНАЧ(v)-PHAЧ(v).
Значение PE3EPB(v) равно максимальной задержке в выполнении работы v, не влияющей на плановый срок Т. Понятно, что справедливо и такое равенство
РЕЗЕРВ(v)=ПВЫП(v)-РВЫП(v).
| Работы | РНАЧ | РВЫП | ПНАЧ | ПВЫП | Резерв |
Рис 6.7. Численные характеристики сетевого графика
Работы, имеющие нулевой резерв времени, называются критическими. Через любую такую работу проходит некоторый максимальный s-t-путь в сети G. Поэтому такой метод нахождения критических работ и называют методом критического пути. Критические работы характеризуются тем, что любая задержка в их выполнении автоматически ведет к увеличению времени выполнения всего проекта.
Численные значения введенных характеристик сетевых графиков для проекта из рис.6.6 даны на рис. 6.7. Расчеты выполнены при Т=20. Критическими работами этого проекта являются работы с номерами 0,1,2,4,6,8, которые и образуют в сети G критический путь.
Исследование сетевых графиков на этом мы завершим. Отметим только, что помимо рассмотренных нами характеристик, часто рассматривают и большое число других, связанных, например, с неопределенностью во времени выполнения работ, с управлением ресурсами и т.д. Достаточно обширный и содержательный материал по этому поводу можно найти в книге [8].
Дата добавления: 2021-07-22; просмотров: 578;











