Плоскопараллельное движение

Плоскопараллельным называется такое движение абсолютно твёрдого тела, при котором скорости всех его точек параллельны некоторой неподвижной плоскости .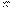

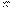- плоскость (х1,х2)||( y1,y2).

По формуле Эйлера:

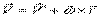
Так как 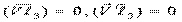, то

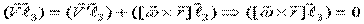
(круговая перестановка - )

или .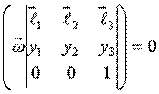

Т. е. скалярное произведение векторов :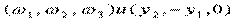

.

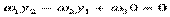В силу произвольности координат y1, y2 точки Р =>

.

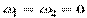Итак: вектор мгновенной угловой скорости расположен на оси .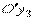

Обычно рассматривают плоское сечение тела || 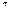- фигуру S.

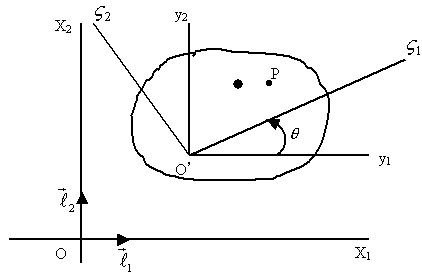
Рис.43.

Положение S определяется тремя параметрами:

1) 2 – е координаты точки О’,

2) 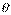- угол поворота жёстко связанных осей (рис. 43).

Для точки Р в плоскости ( ):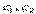

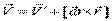, где .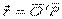

Или (совместив с О):

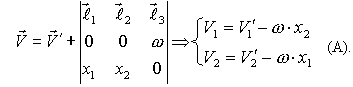
Так как точка в каждый момент времени, в которой скорость в этот момент равна нулю.

Пусть это О*(х1*, х2*).

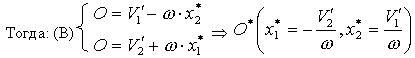
То есть если 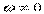, то единственная точка, скорость которой равна нулю. Вычитая (В) из (А) получим:

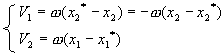
Если поместить начало координат в точку О*, то в этот момент времени распределение скоростей точек будет таким же, как во вращательном движении вокруг неподвижной оси. Точка О* называется центром мгновенного вращения, или мгновенным центром скоростей.

Пример: нахождение центра мгновенного вращения, если известно направление скоростей двух точек тела (рис. 44).

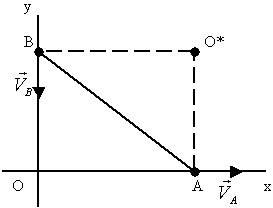
Рис.44.

Обратное рассуждение:

Если центр найден, то все скорости направлены 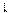радиусу - вектору. Поэтому (обратно) для нахождения центра надо проводить 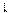к скоростям до пересечения.

Пример: палочка АВ = l скользит по прямым Ох и Oy.

По формуле Ривальса можно найти распределение ускорений, мгновенный центр ускорений, а так же вычислить ускорение центра мгновенного вращения (и скорость мгновенного центра ускорений).

Контрольные вопросы:

1. Какое движение твёрдого тела называется плоскопараллельным?

2. Что такое мгновенный центр скоростей?

3. Как найти мгновенный центр скоростей, если известны скорости двух точек твёрдого тела?