Применение локального элиминационного алгоритма

Рассмотрим решение подзадачи, соответствующей блоку 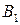(рис. 8.11). Поскольку этот блок связан с блоком 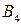, нам нужно решить задачу ДО с переменными для всех возможных наборов переменных . Таким образом, по­сколь­ку 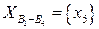, а 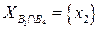, то подзадача имеет вид:

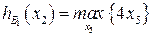
при ограничениях

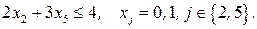
Решение задачи запишем в виде следующей таблицы:

Таблица 8.16. Вычисление .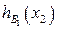

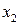
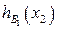
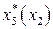
Следующая подзадача, соответствующая листу дерева клик ‑ блоку 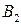, имеет вид:

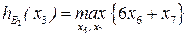
при ограничениях

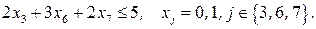
Решение этой подзадачи:

Таблица 8.17. Вычисление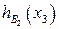

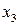
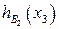
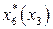
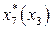
Рис. 8.11. Древовидная декомпозиция для примера 8.1.

Подзадача, соответствующая блоку 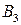, имеет вид:

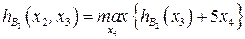
при ограничениях

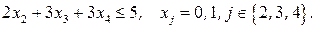
Таблица 8.18. Вычисление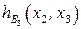

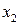
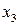
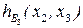
Последняя подзадача, имеет вид:

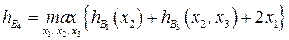
при ограничениях

Таблица 8.19. Вычисление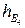

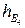
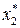
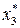
Итак, оптимальное значение целевой функции равно 18. Найдем оптимальные значения переменных, используя таблицы 8.16‑8.19: 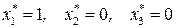(таблица 8.19). Из таблицы 8.18, учитывая, что 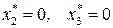, найдем 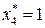. Из таблицы 8.17, учитывая, что 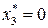, найдем 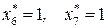. Из таблицы 8.16, учитывая, что 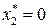, найдем 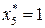. Итак, найдено оптимальное решение: (1, 0, 0, 1, 1, 1, 1); оптимальное значение ЦФ равно 18.

[1] Кочетов Ю. А. Вычислительные возможности локального поиска в комбинаторной оптимизации // Журнал вычислительной математики и математической физики. ‑ 2008. ‑ Т. 48. ‑ C. 747–764.

[2] Dantzig G. B. Time-staged methods in linear programming. Comments and early history // Large-Scale Linear Programming / G. B. Dantzig, M. A. H. Dempster and M. J. Kallio, eds. ‑ Laxenburg: International Institute for Applied Systems Analysis, 1981. ‑ P. 3-16.

[3] Щербина О. А. О задаче оптимизации предварительного резервирования гостиничных номеров // Исследование операций и АСУ. ‑ Киев: КГУ. ‑ 1976. ‑ Вып. 7. ‑ С. 105-112.

[4] The Temporal Knapsack Problem and its solution / M. Bartlett [et al.] // Second International Conference on the Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems (CPAIOR, May 2005). P. 34-48.

[5] Пропой А. И. Элементы теории дискретных оптимальных процессов. ‑ М.: Наука, 1973. ‑ 256 с.

[6] Супер-вершина (supernode) ‑ множество обыч­ных вер­шин, которая может рассматриваться НСЛА декомпозиции как одна вершина.

[7] Parter S. The use of linear graphs in Gauss elimination // SIAM Review. ‑ 1961. ‑ V. 3. ‑ P. 119-130.

[8] Liu J. W. H. The role of elimination trees in sparse factorization // SIAM Journal on Matrix Analysis and Applications. ‑ 1990. ‑ V. 11. ‑ P. 134-172.

[9] Karypis G., Kumar V. MeTiS - a software package for partitioning unstructured graphs, partitioning meshes, and computing fill-reducing orderings of sparse matrices. Version 4. University of Minnesota, 1998.

URL: http://www-users.cs.umn.edu/~karypis/metis