Конденсированный структурный граф
Если задача ДО разбита на блоки, соответствующие подмножествам переменных (называемых супер-переменными), то полученная блочная структура может быть описана с помощью структурного конденсированного графа, супер-вершины которого соответствуют подмножествам переменных (или блокам) исходного графа и супер-ребра соответствуют соседним блокам. При решении задач ДО с помощью ЛЭА, элиминация переменных целесообразна в случае достаточно большой разреженности их графов взаимосвязей, поскольку вычислительная сложность элиминации переменной 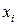 на шаге
на шаге 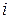 пропорциональна
пропорциональна 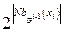 .
.
Использование метода сжатия подмножеств переменных в супер-переменные позволяет получить конденсированные или супер-задачи ДО, имеющие более простую структуру (например, древовидную), которые могут быть решены более эффективно.
Структурный граф супер-задачи ДО получается с помощью представления множества «сжатых» вершин в виде одной супер-вершины и соединения супер-вершины со всеми вершинами, которые были смежны некоторым из сжатых вершин. Этот граф обычно называется фактор-графом.
Упорядоченным разбиением множества 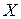 называется декомпозиция
называется декомпозиция 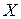 в виде упорядоченной последовательности попарно непересекающихся непустых подмножеств, объединение которых – все множество
в виде упорядоченной последовательности попарно непересекающихся непустых подмножеств, объединение которых – все множество 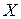 .
.
Разбиение является фундаментальной задачей на графах. Одним из вариантов этой задачи состоит в разбиении множества вершин 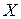 на три множества
на три множества 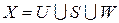 , такие, что
, такие, что 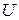 и
и 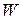 являются сбалансированными, т.е. ни одно из них не слишком мало, а
являются сбалансированными, т.е. ни одно из них не слишком мало, а 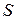 невелико. Удаление
невелико. Удаление 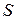 вместе со всеми ребрами, инцидентными его вершинам, разбивает граф на два несвязных компонента.
вместе со всеми ребрами, инцидентными его вершинам, разбивает граф на два несвязных компонента. 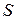 называется сепаратором. В общем случае задача разбиения графа является NP-трудной. Поскольку задача разбиения графа является трудной, возникает необходимость разработки приближенных алгоритмов. Популярным алгоритмом этого рода является MeTiS[9], имеющий хорошую бесплатную программную реализацию.
называется сепаратором. В общем случае задача разбиения графа является NP-трудной. Поскольку задача разбиения графа является трудной, возникает необходимость разработки приближенных алгоритмов. Популярным алгоритмом этого рода является MeTiS[9], имеющий хорошую бесплатную программную реализацию.
Важным частным случаем разбиений являются так называемые блоки. Две вершины называются неразличимыми, если они имеют одинаковые замкнутые окрестности. Блок – максимальное множество неразличимых вершин. Понятно, что блоки не пересекаются и образуют разбиение графа. Соответствующий фактор-граф называется конденсированным графом, часто дающим более сжатое представление структуры исходного графа. Неформально, конденсированный граф образуется с помощью слияния всех вершин с одинаковыми окрестностями в одну вершину (супер-вершину) и слияния полученных множественных ребер.
Блоки графа 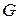 образуют разбиение
образуют разбиение 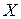 , так как неразличимость является отношением эквивалентности, определенным на исходных вершинах.
, так как неразличимость является отношением эквивалентности, определенным на исходных вершинах.
Отношение эквивалентности на множестве порождает его разбиение, а любое разбиение порождает отношение эквивалентности. Для данного графа 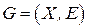 обозначим через
обозначим через 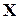 разбиение множества вершин
разбиение множества вершин 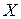 :
: 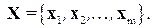
Это означает, что 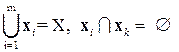 для
для 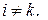 Определим фактор-граф графа
Определим фактор-граф графа 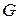 по отношению к разбиению
по отношению к разбиению 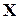 в виде следующего графа
в виде следующего графа
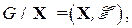
где 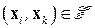 тогда и только тогда, когда
тогда и только тогда, когда 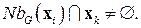
Фактор-граф 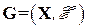 является эквивалентным представлением графа взаимосвязей
является эквивалентным представлением графа взаимосвязей 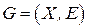 , где
, где 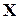 ‑ множество блоков (или множеств неразличимых вершин), а
‑ множество блоков (или множеств неразличимых вершин), а 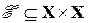 ‑ ребра, определенные на
‑ ребра, определенные на 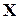 . Схема локальной блочной элиминации является элиминационной процедурой, в которой вершины каждого блока элиминируются одновременно, кластером. В качестве приложения метода кластеризации рассмотрим процедуру локальной блочной элиминации, в которой элиминация блока (т.е. подмножества переменных) может рассматриваться как элиминация супер-переменной.
. Схема локальной блочной элиминации является элиминационной процедурой, в которой вершины каждого блока элиминируются одновременно, кластером. В качестве приложения метода кластеризации рассмотрим процедуру локальной блочной элиминации, в которой элиминация блока (т.е. подмножества переменных) может рассматриваться как элиминация супер-переменной.
Выполненные сжатия множеств вершин определяют на множестве соответствующих переменных так называемое дерево синтеза ‑ дерево, листья которого соответствуют переменным исходной задачи ДО 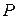 , а промежуточные вершины являются супер-переменными, соответствующими комбинациям вершин-потомков. Используя дерево синтеза, возможно осуществить «декодирование» супер-переменных и найти решение исходной задачи ДО.
, а промежуточные вершины являются супер-переменными, соответствующими комбинациям вершин-потомков. Используя дерево синтеза, возможно осуществить «декодирование» супер-переменных и найти решение исходной задачи ДО.
Рассмотрим упорядоченное разбиение 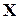 множества
множества 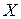 переменных на блоки:
переменных на блоки:
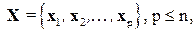
где 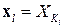 (
( 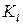 ‑ множество индексов, соответствующих
‑ множество индексов, соответствующих 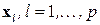 ).
).
Для этого упорядоченного разбиения 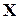 , задача ДО P: (8.1) ‑ (8.3) может быть решена с помощью ЛЭА, используя фактор-граф взаимосвязей
, задача ДО P: (8.1) ‑ (8.3) может быть решена с помощью ЛЭА, используя фактор-граф взаимосвязей 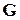 .
.
A. Прямая часть
Рассмотрим вначале блок 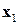 . Тогда
. Тогда
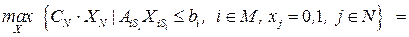
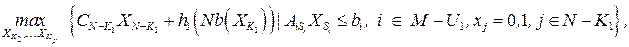 где
где 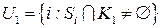 и
и
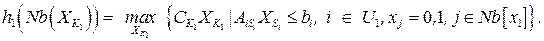
Первый шаг локальной блочной элиминационной процедуры состоит в решении, используя полный перебор значений 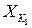 , следующей задачи оптимизации
, следующей задачи оптимизации
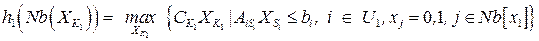
и запоминании оптимальных локальных решений 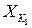 в виде функций окрестностей
в виде функций окрестностей 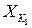 , т.е.
, т.е. 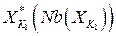 .
.
Максимизация 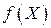 по всем возможным присвоениям
по всем возможным присвоениям 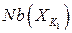 , называется элиминацией блока (или элиминацией супер-переменной)
, называется элиминацией блока (или элиминацией супер-переменной) 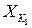 . После элиминации
. После элиминации 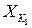 необходимо решить задачу оптимизации:
необходимо решить задачу оптимизации:
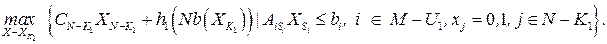 Заметим, что эта задача имеет тот же вид, что и исходная задача, а табличная функция
Заметим, что эта задача имеет тот же вид, что и исходная задача, а табличная функция 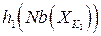 может быть рассмотрена как новый компонент измененной целевой функции. Следовательно, та же процедура может быть использована для поочередной элиминации блоков – супер-переменных
может быть рассмотрена как новый компонент измененной целевой функции. Следовательно, та же процедура может быть использована для поочередной элиминации блоков – супер-переменных 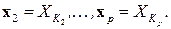 На каждом шаге
На каждом шаге 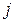 запоминаются новый компонент
запоминаются новый компонент 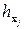 и оптимальные локальные решения
и оптимальные локальные решения 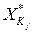 в виде функций от
в виде функций от 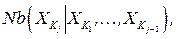 т.е. от множества переменных, взаимосвязанных по крайней мере с одной переменной из
т.е. от множества переменных, взаимосвязанных по крайней мере с одной переменной из 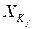 в текущей задаче, полученной из исходной задачи с помощью элиминации
в текущей задаче, полученной из исходной задачи с помощью элиминации 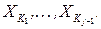 Так как множество
Так как множество 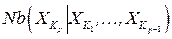 пустое, элиминация
пустое, элиминация 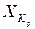 позволит получить оптимальное значение целевой функции
позволит получить оптимальное значение целевой функции 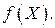
B. Обратная часть.
Эта часть процедуры состоит в последовательном выборе 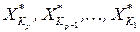 ‑ оптимальных локальных решений из сохраненных в прямой части таблиц
‑ оптимальных локальных решений из сохраненных в прямой части таблиц
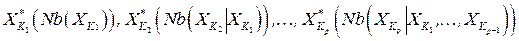 .
.
Дата добавления: 2016-06-05; просмотров: 2698;











