Локальные алгоритмы элиминации переменных, использующие в качестве структурного графа граф взаимосвязей переменных задачи.
Рассмотрим решение разреженной дискретной задачи оптимизации (8.8) – (8.10), структура которой описывается неориентированным графом взаимосвязей переменных 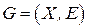 , с помощью локального алгоритма элиминации переменных. ЛЭА использует упорядочение вершин графа.
, с помощью локального алгоритма элиминации переменных. ЛЭА использует упорядочение вершин графа.
В дальнейшем с целью упрощения обозначений будем использовать упорядочение 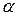 для индексирования множества вершин
для индексирования множества вершин 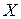 графа
графа 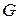 , т.е.
, т.е. 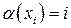 и
и 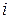 будет рассматриваться как индекс или метка вершины
будет рассматриваться как индекс или метка вершины 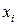 .
. 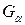 и
и 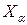 обозначают соответственно упорядоченный граф и упорядоченное множество вершин.
обозначают соответственно упорядоченный граф и упорядоченное множество вершин.
Для данного упорядочения 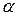 вершин графа
вершин графа 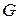 в виде
в виде 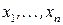 через
через 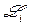 обозначим множество вершин с индексами из
обозначим множество вершин с индексами из 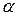 , большими
, большими 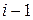 :
: 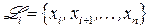 .
.
Определение 8.8. Монотонной окрестностью вершины 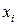 называется множество вершин, соседних с
называется множество вершин, соседних с 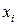 , с индексами, большими, чем
, с индексами, большими, чем 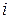 (согласно упорядочению
(согласно упорядочению 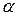 ):
):
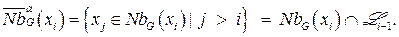
Определение 8.9. Граф, полученный из графа 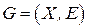 с помощью
с помощью
· удаления вершины 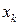 и всех ребер, исходящих из нее и
и всех ребер, исходящих из нее и
· соединения ребрами всех ранее не соседних вершин в 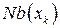 , называется
, называется 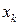 -элиминационным графом графа
-элиминационным графом графа 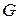 и обозначается
и обозначается 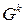 .
.
Описанная операция называется элиминацией вершины 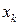 .
.
Для данного упорядочения 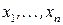 работа ЛЭА состоит в последовательной элиминации вершин
работа ЛЭА состоит в последовательной элиминации вершин 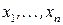 в текущем графе и вычислении соответствующей локальной информации о вершинах
в текущем графе и вычислении соответствующей локальной информации о вершинах 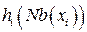 . Этот процесс порождает последовательность элиминационных графов:
. Этот процесс порождает последовательность элиминационных графов: 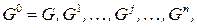 так что
так что 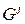 ‑
‑ 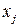 -элиминационный граф графа
-элиминационный граф графа 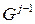 , а
, а 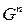 ‑ пустой граф.
‑ пустой граф.
Процесс преобразования графа взаимосвязей переменных, соответствующий процедуре элиминации переменных с помощью локального алгоритма, известен как «элиминационная игра», которая впервые была введена Партером, как графовая интерпретация метода исключения Гаусса. Входом для алгоритма элиминационной игры является граф 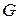 и упорядочение
и упорядочение 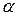 графа
графа 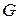 .
.
Одним из методов, позволяющим решать задачи ДО (P), является локальный алгоритм (ЛА) А, описанный в разделе 8.2.2. Одним из недостатков ЛА А является то, что он не решает до конца задачу дискретной оптимизации, а лишь упрощает ее (в отдельных случаях). Кроме того, между ЛА А и ЛА A, решающим квазиблочные задачи ДО, не видно явной связи.
Рассмотрим модификацию алгоритма A, несериальный ЛА (НСЛА), использующий парадигму динамического программирования (ДП) и позволяющий полностью решать задачи ДО путем элиминации переменных.
Рассмотрим задачу (P) ДО вида (8.8) – (8.10), структура которой задается графом 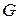 взаимосвязей. Введем следующие обозначения для множеств вершин
взаимосвязей. Введем следующие обозначения для множеств вершин 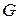 :
:
· Смежность множеств: 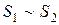 (читается «
(читается « 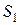 смежно
смежно 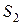 »), если существует вершина
»), если существует вершина 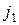 в
в 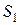 и вершина
и вершина 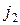 в
в 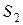 такие, что
такие, что 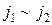 .
. 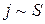 означает
означает 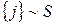 .
.
· Окрестность множества вершин 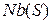 =
= 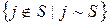 . Замкнутая окрестность множества
. Замкнутая окрестность множества 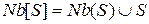 .
.
· Внутренность множества 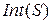 =
= 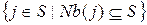 .
.
· Граница множества 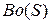 =
= 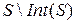 .
.
Для переменных задачи ДО будем использовать все эти же обозначения, пользуясь взаимно-однозначным соответствием между вершинами графа взаимосвязей и переменными.
Локальный алгоритм элиминации переменных в задаче ДО состоит в последовательном исключении (элиминировании) переменных, причем порядок, в котором переменные будут исключаться, важен, так как он существенно влияет на объем вычислений.
Рассмотрим описанную выше задачу ДО (P). Предположим без потери общности, что переменные исключаются в порядке 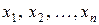 . Рассмотрим исключение первой переменной
. Рассмотрим исключение первой переменной 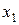 . Найдем члены целевой функции, содержащие
. Найдем члены целевой функции, содержащие 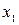 :
: 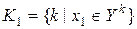 и множество индексов ограничений, содержащих
и множество индексов ограничений, содержащих 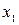 :
: 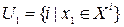 . Совместно с
. Совместно с 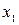 в
в 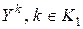 и в
и в 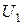 входят переменные из
входят переменные из 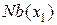 . Переменной
. Переменной 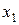 соответствует следующая подзадача
соответствует следующая подзадача 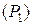 :
:
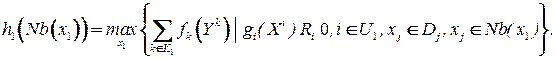
Тогда исходная задача (P) сводится к решению следующей задачи:
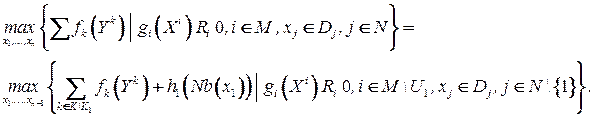
В последней задаче 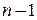 переменная, по сравнению с исходной задачей (P) из ограничений исключены ограничения с индексами из
переменная, по сравнению с исходной задачей (P) из ограничений исключены ограничения с индексами из 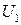 , а также члены целевой функции
, а также члены целевой функции 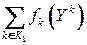 , однако появился новый член целевой функции
, однако появился новый член целевой функции 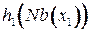 , благодаря чему изменился граф взаимосвязей задачи: в нем вершина
, благодаря чему изменился граф взаимосвязей задачи: в нем вершина 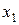 удалена, а вершины из
удалена, а вершины из 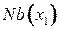 соединены ребрами между собой (благодаря члену
соединены ребрами между собой (благодаря члену 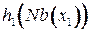 (содержащий вычисленную информацию), связавшему эти вершины между собой). Это называется «пополнением» (fill). Заметим, что вершины из
(содержащий вычисленную информацию), связавшему эти вершины между собой). Это называется «пополнением» (fill). Заметим, что вершины из 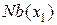 образуют так называемую клику графа
образуют так называемую клику графа 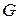 [6].
[6].
Новый граф взаимосвязей обозначим 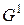 . Далее все окрестности переменных находятся уже в новом графе
. Далее все окрестности переменных находятся уже в новом графе 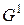 . Алгоритм исключает оставшиеся переменные по одной за раз аналогичным образом. Будем предполагать, что переменные перенумерованы так, что они исключаются следующим образом:
. Алгоритм исключает оставшиеся переменные по одной за раз аналогичным образом. Будем предполагать, что переменные перенумерованы так, что они исключаются следующим образом: 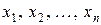 . Исключение очередной переменной
. Исключение очередной переменной 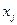 называется «шаг
называется «шаг 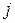 », а функции (таблицы), вычисленные на этом шаге, будем обозначать
», а функции (таблицы), вычисленные на этом шаге, будем обозначать 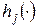 .
.
ЛЭА может быть кратко записан так:
1. Перенумеровать переменные согласно порядку 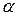 (в данном случае
(в данном случае 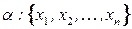 ).
).
2. Для 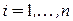 исключить
исключить 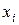 , изменяя граф взаимосвязей путем добавления ребер для превращения окрестности исключаемой вершины в клику.
, изменяя граф взаимосвязей путем добавления ребер для превращения окрестности исключаемой вершины в клику.
Пример 8.1 (продолжение).
Рассмотрим решение задачи ДО (8.11)- (8.15) из примера 8.1. Обозначим 
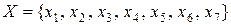 ‑ множество всех переменных задачи; подмножества
‑ множество всех переменных задачи; подмножества 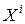 переменных, входящих в ограничения (8.12)- (8.15):
переменных, входящих в ограничения (8.12)- (8.15): 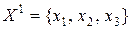 ;
; 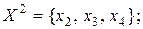
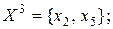
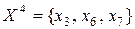 .
.
Построим граф взаимосвязей этой задачи, сопоставляя каждой переменной задачи вершину графа и соединяя 2 вершины ребром, если соответствующие вершинам переменные взаимосвязаны, т.е. входят в одно и то же ограничение или, другими словами, входят в одно и то же подмножество 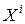 . Так, вершины графа, соответствующие переменным
. Так, вершины графа, соответствующие переменным 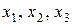 , попарно соединены друг с другом ребрами, так как эти переменные входят в подмножество
, попарно соединены друг с другом ребрами, так как эти переменные входят в подмножество 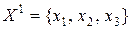 ; вершины для переменных
; вершины для переменных 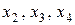 также попарно соединены друг с другом ребрами, так как эти переменные входят в подмножество
также попарно соединены друг с другом ребрами, так как эти переменные входят в подмножество 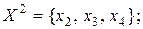 то же можно сказать и о вершинах графа для переменных из подмножества
то же можно сказать и о вершинах графа для переменных из подмножества 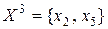 и подмножества
и подмножества 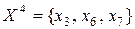 . В то же время не существует ребер графа, связывающих вершины
. В то же время не существует ребер графа, связывающих вершины 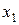 и
и 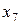 , так как эти переменные не входят одновременно ни в одно из подмножеств
, так как эти переменные не входят одновременно ни в одно из подмножеств 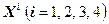 .
.
Как было отмечено выше, ЛА элиминации переменных состоит в последовательном исключении переменных. Начнем с исключения переменной 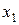 . Для этого проанализируем, используя граф взаимосвязей переменных (рис. 8.6 а)), с какими переменными
. Для этого проанализируем, используя граф взаимосвязей переменных (рис. 8.6 а)), с какими переменными 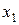 связана ‑ с переменными
связана ‑ с переменными 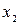 и
и 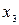 , составляющими окрестность
, составляющими окрестность 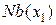 . Заметим, что вершина 1, соответствующая переменной
. Заметим, что вершина 1, соответствующая переменной 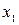 в графе, симплициальна, так как ее соседи (вершины 2 и 3) образуют клику. Построим из исходной задачи задачу оптимизации, содержащую переменную
в графе, симплициальна, так как ее соседи (вершины 2 и 3) образуют клику. Построим из исходной задачи задачу оптимизации, содержащую переменную 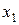 в целевой функции и ограничениях:
в целевой функции и ограничениях:
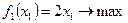

при ограничениях
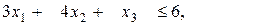 (8.12')
(8.12')
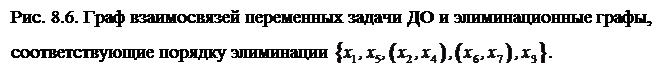
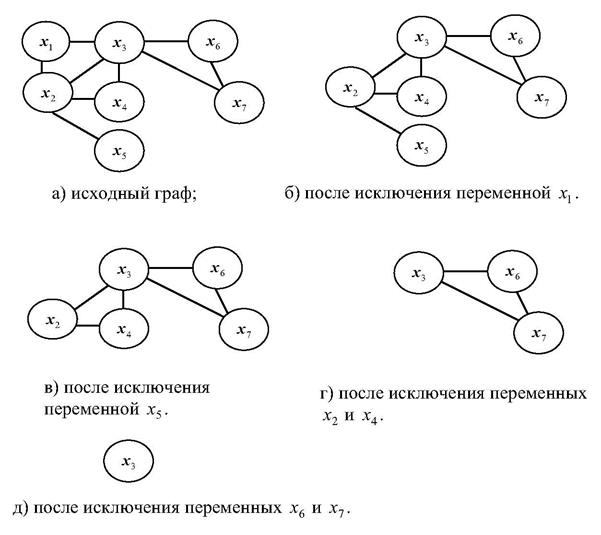
Далее для каждого набора значений переменных 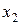 и
и 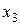 , вычислим значение переменной
, вычислим значение переменной 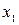 , для которого значение функции
, для которого значение функции 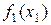 будет максимальным при соблюдении ограничения (8.12'). Вычисления запишем в таблицу 8.1, в которой
будет максимальным при соблюдении ограничения (8.12'). Вычисления запишем в таблицу 8.1, в которой
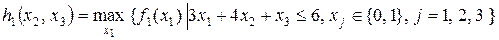
и 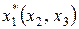 ‑ значение переменной
‑ значение переменной 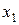 , соответствующее
, соответствующее 
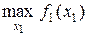 .
.
Таблица8.1. Вычисление
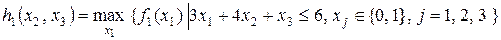
| x2 | x3 | x1 | 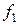
| 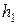
| 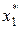
|
| - | |||||
| - |
Замечание. Символом «-» обозначено отсутствие допустимых решений.
Заметим, что здесь мы пользовались принципом оптимальности Беллмана, поскольку из всех возможных значений 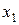 выбрали для каждого набора
выбрали для каждого набора 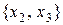 значение
значение 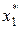 , соответствующее максимуму
, соответствующее максимуму
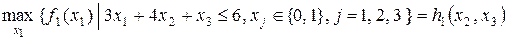 .
.
Следуя обычной процедуре динамического программирования, рассмотрим новую задачу (P1), в которой уже нет исключенной переменной 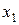 :
:
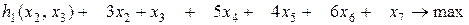
при ограничениях
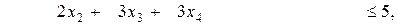 (8.13')
(8.13')
 (P1) (8.14')
(P1) (8.14')
 (8.15')
(8.15')
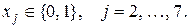
Построим граф взаимосвязей этой новой задачи – элиминационный граф 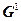 (рис. 8.6 б)).
(рис. 8.6 б)).
Исключим на следующем шаге переменную 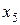 . Для этого найдем окрестность
. Для этого найдем окрестность 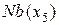 , используя граф взаимосвязей переменных (рис. 8.6 б)):
, используя граф взаимосвязей переменных (рис. 8.6 б)): 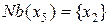 .
.
Построим задачу оптимизации, содержащую переменную 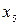 в целевой функции и ограничениях:
в целевой функции и ограничениях:
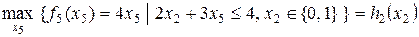
Вычисления запишем в таблицу 8.2, в которой 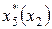 ‑ значение переменной
‑ значение переменной 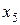 , соответствующее
, соответствующее 
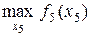 .
.
Таблица 8.2. Вычисление
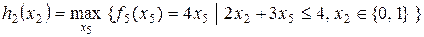 .
.
| x2 | x5 | 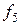
| 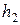
| 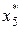
|
| - |
Рассмотрим новую задачу (P2), в которой уже нет переменной 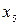 и ограничения (8.12') (учтенного в функции
и ограничения (8.12') (учтенного в функции 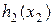 )
)
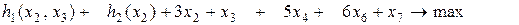
при ограничениях
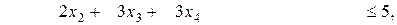 (8.14'')
(8.14'')
 (8.15'')
(8.15'')
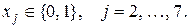
Граф взаимосвязей этой задачи показан на рис. 8.6 в).
Покажем возможность исключения сразу нескольких переменных (блока переменных). Анализируя граф взаимосвязей на рис. 8.6 в) и замечая, что 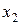 и
и 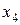 связаны лишь с
связаны лишь с 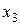 (в ограничении (8.14'') и целевой функции), исключим их вместе (блоком), построив таблицу 8.3 для решения следующей оптимизационной задачи:
(в ограничении (8.14'') и целевой функции), исключим их вместе (блоком), построив таблицу 8.3 для решения следующей оптимизационной задачи:
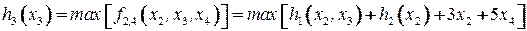
при ограничениях
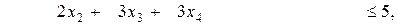
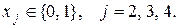
Таблица 8.3. Вычисление
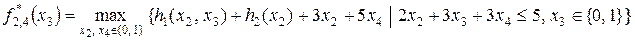 .
.
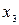
| 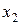
| 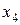
| 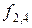
| 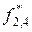
| 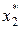
| 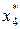
|
| - | ||||||
| - |
В результате получим новую задачу (P3), из которой исключен блок переменных 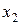 и
и 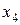 :
:
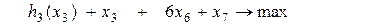
при ограничениях
 (8.15''')
(8.15''')
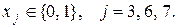
Анализируя новый граф взаимосвязей на рис. 8.6 г) и замечая, что 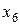 и
и 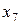 связаны лишь с
связаны лишь с 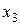 (в ограничении (8.15''') и целевой функции), исключим их вместе (блоком), построив таблицу 8.4 для решения следующей оптимизационной задачи:
(в ограничении (8.15''') и целевой функции), исключим их вместе (блоком), построив таблицу 8.4 для решения следующей оптимизационной задачи:
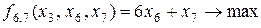
при ограничениях

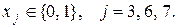
В результате получим новую задачу (P4), из которой исключен блок переменных 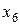 и
и 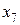 :
:
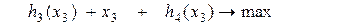
при ограничениях 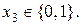
Решение последней задачи осуществляется сравнением значений целевой функции при 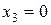 и
и 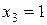 (табл. 8.5).
(табл. 8.5).
Таблица 8.4. Вычисление
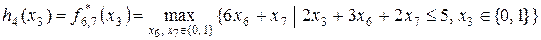 .
.
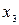
| 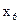
| 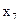
| 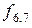
| 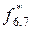
| 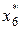
| 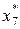
|
| - |
Таблица 8.5. Вычисление 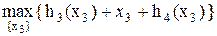 .
.
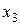
| 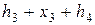
| 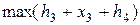
| 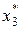
|
Из таблицы 8.5 получаем решение 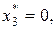 соответствующее максимальному значению целевой функции 18 исходной задачи. Порядок исключения переменных в приведенном примере:
соответствующее максимальному значению целевой функции 18 исходной задачи. Порядок исключения переменных в приведенном примере: 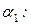 {x1, x5, (x2, x4), (x6, x7), x3}. Можно убедиться, что исключение переменных в другом порядке, например,
{x1, x5, (x2, x4), (x6, x7), x3}. Можно убедиться, что исключение переменных в другом порядке, например, 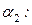 {x3, x6, x7, x2, x1, x4, x5}, приводит к другому объему вычислений.
{x3, x6, x7, x2, x1, x4, x5}, приводит к другому объему вычислений.
Таким образом, в рассматриваемом примере применялся принцип оптимальности Беллмана, для нахождения максимального значения целевой функции были построены таблицы. Чтобы найти само решение (значения переменных), нужно сделать обратный шаг процедуры динамического программирования, анализируя таблицы в обратном порядке. Так, из таблицы 8.5 находим оптимальное значение 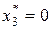 . Возвращаясь к таблице 8.4, находим для
. Возвращаясь к таблице 8.4, находим для 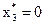 значения переменных
значения переменных 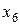 и
и 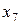 :
: 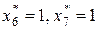 . Из таблицы 8.3 находим, что значению
. Из таблицы 8.3 находим, что значению 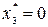 соответствуют
соответствуют 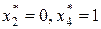 . Таблица 8.2 дает для значения
. Таблица 8.2 дает для значения 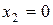 соответствующее
соответствующее 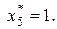 Зная
Зная 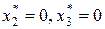 , из таблицы 8.1 получим
, из таблицы 8.1 получим 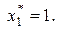 Итак, искомое решение
Итак, искомое решение 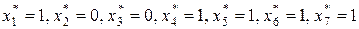 , для которого достигается максимум целевой функции, равный 18.
, для которого достигается максимум целевой функции, равный 18.
К недостаткам описанного выше локального алгоритма элиминации переменных следует отнести то, что на каждом шаге он перебирает значения для всех переменных из исследуемой окрестности 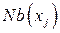 , а ЛА A ‑ лишь значения переменных из граничного множества
, а ЛА A ‑ лишь значения переменных из граничного множества 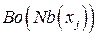 . Ниже предлагается модификация ЛА элиминации переменных, сочетающая достоинства обоих алгоритмов.
. Ниже предлагается модификация ЛА элиминации переменных, сочетающая достоинства обоих алгоритмов.
Как мы уже отметили, ЛА элиминации переменных исследует окрестность 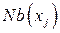 некоторой переменной
некоторой переменной 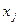 и находит для всех значений переменных из этой окрестности оптимальное значение
и находит для всех значений переменных из этой окрестности оптимальное значение 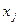 , что может приводить к большому объему вычислений. Однако переменные из окрестности могут обладать разными свойствами по отношению к своей окрестности: одни из них имеют связи лишь с переменными из данной окрестности, другие же связаны и с переменными извне. Поэтому имеет смысл осуществлять полный перебор значений лишь для переменных, принадлежащих границе окрестности
, что может приводить к большому объему вычислений. Однако переменные из окрестности могут обладать разными свойствами по отношению к своей окрестности: одни из них имеют связи лишь с переменными из данной окрестности, другие же связаны и с переменными извне. Поэтому имеет смысл осуществлять полный перебор значений лишь для переменных, принадлежащих границе окрестности 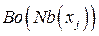 , как в ЛА A, а оптимальные значения «внутренних» переменных окрестности (т. е. переменных из
, как в ЛА A, а оптимальные значения «внутренних» переменных окрестности (т. е. переменных из 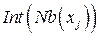 ) определять совместно с переменной
) определять совместно с переменной 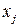 , образуя «блок» переменных. В ЛА элиминации переменных переменные из
, образуя «блок» переменных. В ЛА элиминации переменных переменные из 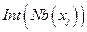 могут рассматриваться как «блочная» переменная (или супер-переменная). Переменные в упорядочении
могут рассматриваться как «блочная» переменная (или супер-переменная). Переменные в упорядочении 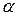 , принадлежащие к
, принадлежащие к 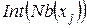 , могут рассматриваться также как одна блочная переменная, проиндексированная переменной
, могут рассматриваться также как одна блочная переменная, проиндексированная переменной 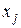 . При построении блочных переменных целесообразно использовать понятие «супер-вершины» [6], объединяющей в себе так называемые «неразличимые вершины» (в графе G две смежные вершины u и v называются неразличимыми, если
. При построении блочных переменных целесообразно использовать понятие «супер-вершины» [6], объединяющей в себе так называемые «неразличимые вершины» (в графе G две смежные вершины u и v называются неразличимыми, если 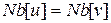 ).
).
Рассматривая квазиблочную задачу ДО, можно объединить все «внутренние» переменные блоков, являющиеся неразличимыми, в супер-вершины, соответствующие блокам, при этом общие переменные блоков (переменные из «перемычек») образуют другие супер-вершины. В результате решение квазиблочной задачи ДО c помощью блочной модификации НСЛА сводится к решению задачи с линейным графом вида 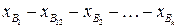 и реализация этого алгоритма совпадает с ЛА A.
и реализация этого алгоритма совпадает с ЛА A.
8.3.5. Графовые структуры локального элиминационного алгоритма
Дата добавления: 2016-06-05; просмотров: 1888;











